Signaalinkäsittelytekniikan laboratorio
Digitaalitekniikan perusteet - luento 10
Mooren vs. Mealyn kone -toteutus sekvenssipiirille
Käsitellään esimerkin valossa kahta eri toteutustapaa Mooren konetta ja Mealyn konetta
Muistutukseksi / kertauksena:
Mooren koneessa ovat kaikki antosignaalit riippuvat vain piirin tilasta. Kaikki annot on siis ASM-kaaviossa merkitty suorakulmioiden sisään.
Mealyn koneessa esiintyy myös ehdollisia antoja eli antosignaali riippuu sekä piirin tilasta että ottosignaaleista. Tämähän merkittiiin ASM-kaaviossa päätöslohkon jälkeen pyöristetyn suorakulmion sisään.
Kun valitaan Mooren ja Mealyn kone- toteutuksen välillä muistetaan vielä, että Mooren kone -toteutuksessa on yleensä enemmän tiloja, mutta kombinaatiopiiri saattaa olla Mealyn kone -toteutusta yksinkertaisempi
Tehtävä
Tehtävän anto on monimutkaistaa aikaisemmin
esitettyä valomainosta siten, että siihen tulee yksi toiminto lisää. (Tähän mennessähän vaihtoehtoja oli kaksi:
joko kaikki sanat palavat koko ajan tai mainos kiertää vanhaa tilaketjua normaalisti). Lisätään näihin vaihtoehtoihin
vielä yksi vaihtoehto:
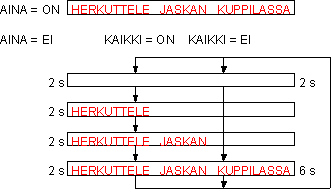
jos ottosignaali KAIKKI = 0, kierretään pelkästään tilaketjua tyhjä taulu --> kaikki sanat taulullla --> tyhjä taulu.
Jos
KAIKKI = 1, kierretään normaalia tilaketjua. AINA -signaalin toiminta pysyy ennallaan. Kaavio selventänee.
|
|
Piirin toteutus
Mooren kone -toteutus monimutkaiselle valomainokselle
Piirin ASM-kaavion teko lähtee liikkeelle valomainoksen tyhjän taulun tilasta (= EI -tila) seuraavasti:
EI-tilassa pitää haarautua sen mukaan, pysytäänkö entisessä
tilasekvenssissä (tilakierrossa, jossa kaikki valot syttyvät erikseen 2 sekunnin välein) vai mennäänkö tilaan, jossa kaikki valot palavat 6 sekuntia. Näin ollen EI ja HJK (= kaikki sanat palavat) välille
tulee kaksi erilaista tilakiertomahdollisuutta. Molemmat tilakierto mahdollisuudet tarvitsevat kaksi tilaa. Lisäksi tilakierroille on yhteistä ensimmäinen (EI-tila) ja viimeinen (HJK-tila) tila. Tästä johtuen =>
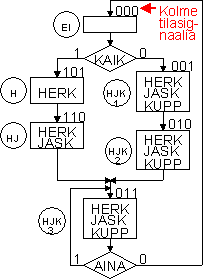
Tilakoneeseen tarvitaan yhteensä kuusi tilaa (ks. ASM-kaavio alla). Tästä johtuen tilakoodin pituudeksi tulee kolme bittiä (joilla saadaaan toteutetuksi 23=8 tilaa):
|
KAIK-signaali määrää EI -tilasta lähdettäessä, kumpaan haaraan mennään. Sekvenssin vaihto
yhden tietyn haaran aikana ei ole mahdollista. (Muitakin toteutusmahdollisuuksia olisi). Piirin lohkokaavio on esitetty alla.
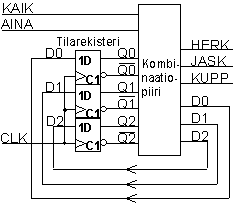
Kiikkuja tarvitaan kolme, koska tilabittejä on 3 (ja tiloja siis 6). Tässä on valittu D-kiikku toteutus, mutta se ei suinkaan ole ainoa vaihtoehto
|
Tilataulukko
|
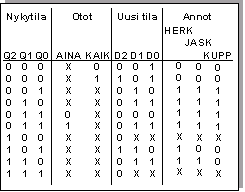
Seuraavaksi muodostetaan ASM-kaaviosta tilataulukko, joka on esitetty vasemmalla. Tilataulukkohan muodostettiin seuraavasti:
Lähdetään ASM-kaavion ensimmäisestä tilasta (tilakoodi = 000), jonka tilakoodii tulee tilataulukon nykytilaksi (Q2, Q1 ja Q0).
Sitten merkataan uudeksi tilaksi (D2, D1 ja D0) sen tilan tilakoodi johon siirrytään (tilakoodi 001), sekä lisäksi annot, jotka vaikuttavat mihin tilaan siirrytään (AINA = X, KAIK=0).
Mikäli ottosignaalilla ei ole merkitystä tilasiirtymään, merkataan sen kohdalle X. (Näin
saadaan tilataulukko lyhyemmäksi ja saadaan sievennysvaiheessa mahdollisesti sievempiä lausekkeita --> kuluu vähemmän portteja.)
Tässä tapauksessa jää kaksi tilaa jää käyttämättömiksi (100, 111), sillä 3:lla tilabitillä saatiin 8 tilaa ja niistä käytetään vain 6. Nämä
tilat otetaan kuitenkin mukaan tilataulukkoon, jotta tilataulukko kuvaisi yksiselitteisesti piirin toiminnan. Lisäksi laitteen täytyy pystyä poistumaan käyttämättömästä tilasta jos se syystä tai toisesta siihen joutuu. Uusi tila määritellään siis siten, että käyttämättömistä
tiloista päästään pois ja palataan johonkin käytössä olevaan tilaan. Tässä tapauksessa siirto on hoidettu s.e. palataan johonkin tilaan, jonka ensimmäinen
bitti on nolla. Muuten ehtoja ei ole asetettu, jotta toiminta ei mutkistaisi piirin toteutusta.
Tilataulun annot, ovat antosignaalit, jotka liittyvät nykytilaan. (Ne saadaan siis ASM-kaavion neliöiden sisältä)
|
Kiikkujen ottosignaalit ja antojen lausekkeet
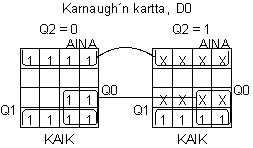
Määritellään Karnaugh'n kartan avulla tilataulukosta lausekkeet D-kiikkujen otoille (jotka ovat siis samat kuin D2, D1 ja D0). Tässä tarvitaan kolme kappaletta 5:en muuttujan Karnaugh'n karttoja, sillä D-ottoja on 3 (D2, D1 ja D0) ja muutuujia on 5 (Q2, Q1, Q0, AINA ja KAIK):
|
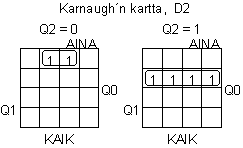
D2 = KAIKQ0'Q1'Q2' + Q0Q1'Q2
|
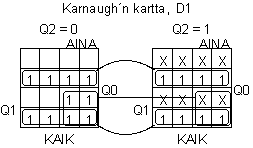
D1 = Q0Q1' + Q0'Q1 + AINAQ1
|
|
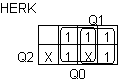 : HERK = Q0 + Q1
|
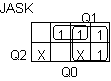 : JASK = Q0Q2' + Q1
|
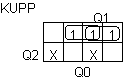 : KUPP = Q0Q2'+ Q1Q2'
|
Kombinaatiopiiri
Mealyn kone -toteutus monimutkaiselle valomainokselle
Kun valomainos toteutetaan Mealyn koneella, tarvitaan tiloja vain neljä (ks. ASM-kaavio). Tämä johtuu siitä, että
antamalla ottosignaalin KAIK vaikuttaa suoraan antosignaaleihin voidaan haluttu toiminta saada aikaan yhdellä ja samalla
tilasekvenssillä (tilakierrolla). Antosignaalia, johon ottosignaali vaikuttaa suoraan sanotaan ehdolliseksi
antosignaaliksi. (Kuvataan kulmistaan pyöristetyllä suorakaiteella.)
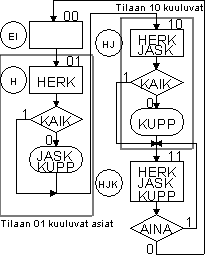
ASM-kaaviota tulkitaan nyt seuraavasti:
Tila 00 - mitään ei näy taululla
Tila 01 - Taululla näkyy HERK. Samalla katsotaan ottosignaalin KAIK arvo. Mikäli tämä on 0 lukee taululla myös JASK KUPP. Muutoin taululla ei lue kuin HERK. ASM-kaavioon on nyt esimerkinomaisesti piirretty neliö, joka näyttää, mitkä kaikki asiat kuuluvat samaan tilaan (eli tapahtuvat samalla ajanhetkellä).
Tila 10 - Taululla lukee HERK JASK. Samalla katsotaan ottosignaalin KAIK arvo. Mikäli tämä on 0 lukee taululla myös KUPP. Muutoin taululla lukee vain HERK JASK.
Tila 11 - Taululla lukee HERK JASK KUPP.
|
Siis H ja HJ tiloissa ottosignaali KAIK vaikuttaa siihen, ovatko muutkin annot kuin tilassa aina aktiiviset
annot päällä vai poissa.
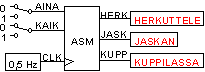
Koska tiloja on vain neljä, pärjätään kahdella kiikulla (22=4)
|
Tilataulukko
Kiikkujen ottosignaalit ja antojen lausekkeet totuustaulun perusteella:
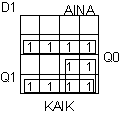 | 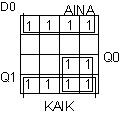 |
D1 = Q0Q1' + Q0'Q1 + Q1AINA
|
|
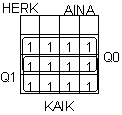 : HERK = Q0 + Q1
|
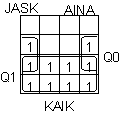 : JASK = KAIK'Q0 + Q1
|
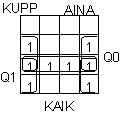 : KUPP = KAIK'Q0+ KAIK'Q1 + Q0Q1
|
Kombinaatiopiiri
Erot toteutusten välillä
| Toteutus | Kiikkuja | Portteja | Porttien ottoja |
|---|
| Moore | 3 - D | 12 | 27 |
| Mealy | 2 - D | 10 | 21 |
| Moore JK | 2 - JK | 8 | 17 |
(JK -kiikkutoteutusta käsitellään vasta seuraavalla sivulla, mutta nähdään, että se säästää huomattavasti
piirin porttien määrässä D -kiikkutoteutuksiin verrattuna.) Samoilla kiikuilla toteutettujen Mooren ja Mealyn
toteutuksen välillä nähdään, että Mealy on taloudellisempi. Mooren kone on kuitenkin luotettavampi ottosignaalivirheiden
suhteen. Valinta
kahden tavan välillä pitää tehdä tapauskohtaisesti.
JK-kiikkujen käyttö sykronisten sekvenssipiirien suunnittelussa
D-kiikussa D-ottoon tuleva signaali määrää suoraan seuraavan tilan (ks. D-kiikun tilataulu aiempaa "kiikku yhteenveto"-kohdasta). Näin ollen tilataulukon sarake
'Uusi tila' riittää sellaisenaan määrittelemään tilakiikkujen D-ottojen lausekkeet. JK-kiikkuja käytettäessä
tilanne on mutkikkaampi. Jokaisen JK-kiikun J- ja K- otoille on muodostettava oma lauseke (eli nyt kussakin kiikussa on kaksi eri ottoa, joiden kombinaatio vaikuttaa uuteen tilaan).
Tehtävän helpottamiseksi kannattaa laatia JK-kiikun tilataulusta toinen versio eli muutostaulu.
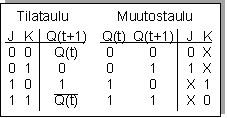
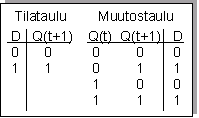
Tämä kuvaa sen, miten missäkin halutussa tilanmuutoksessa ottojen arvot on valittava, jotta haluttu muutos saadaan aikaan. JK -kiikun muutostaulu
esitetään alla. (Vertailun vuoksi oikealla D-kiikun muutostaulu.)
Muutostaulua siis luetaan seuraavasti: Tiedetään nykytila Q(t) ja uusi tila Q(t+1). Millä J:n ja K:n arvoilla saadaan muutos tästä tiedetystä nykytilasta uuteen tilaan aikaiseksi??
|
|
Muutostaulusta nähdään suoraan, mitkä arvot J- ja K- otoille on annettava mitäkin tilanmuutosta
haluttaessa. Muutostaulu havainnollistaa myös sen, miksi usein JK-kiikkutoteutus johtaa yksinkertaisempaan
lopputulokseen kuin D-kiikkutoteutus: Kutakin tilanmuutosta varten on vain joko J- tai K- oton saatava tietty
arvo. Toinen otto voi saada kumman arvon tahansa. Tämä näkyy muutostaulussa X:nä.
Seuraavaksi toteutetaan monimutkaisen valomainoksen Mealyn kone -versio JK -kiikkutoteutuksena.
JK-kiikku - toteutus ei vaikuta mitenkään määrittelyyn, lohkokaavioon tai
tilataulukkoon. Se tulee esille ainoastaan, kun määritellään kiikkujen ottojen lausekkeet ja kun piirretään
piirikaavio.
Tarkastellaan vaikkapa tilataulukon ylintä riviä. Siinä tila muuttuu 00:sta 01:ksi. Q1 ei muutu, vaan pysyy nollana.
Tämä saadaan aikaan muutostaulun mukaisesti asettamalla J1=0 ja K1=X.
Q0 muuttuu nollasta ykköseksi. Tämä taas edellyttää
muutostaulun mukaan, että J=1 ja K=X.
Tarkastellaan vielä harjoituksen vuoksi tilataulukon toinen rivi, jossa tapahtuu tilanmuutos tilasta 01 tilaan 10.
Ensin Q1 muuttuu 0 --> 1. Tämä muutos saadaan JK-kiikulla tehtyä kun J=1 ja K=X
Lisäksi Q0 muuttuu 1 --> 0. Tämä muutos puolestaan saadaan tehtyä kun J=X ja K=0
Tilataulukko käytetään joka rivin osalta vastaavasti.
JK-kiikut sekvenssipiireissä jatkuu..
JK -kiikkujen lausekkeet saadaan edellisen sivun tilataulukosta normaalisti Karnaugh'n karttojen avulla:
Sekä J0 = 1. Nähdään jo tässä, että JK -kiikkutoteutus on yksinkertaisempi kuin
vastaava D-kiikuin toteutettu. Antojen lausekkeet ovat samat kuin D-kiikuilla. Lopullinen
kombinaatiopiiriosan kaavio näyttää tältä:
Maija-pelin valtinarvontakone
Maija-pelissä pata ei voi olla valttia, mutta muuten valtti valitaan pelikohtaisesti. Tässä
esimerkissä suunnitellaan valtinarvontakone, joka antaa satunnaisesti valtiksi joko hertan, ruudun tai ristin.
Arvontakone toteutetaan tilakoneella, jossa on kolme tilaa, yksi kutakin valttikandidaattimaata (hertta, ruutu, risti) kohden.
Sekvenssipiirin kellotaajuudeksi valitaan ihmisen reagointikykyyn nähden suuri arvo, esimerkiksi 100 kHz.
Piiri kiertää kolmessa eri tilassaan 10 mikrosekunnin välein. Piiriin liitetään painike, jonka avulla tilakierto
saadaan pysähtymään siihen tilaan, jossa piiri painamishetkellä oli. Tämä ilmaisee, mikä maa on valttia.
Lisäksi määritellään, että tilaa ilmaiseva lamppu palaa vain nappia painettaessa.
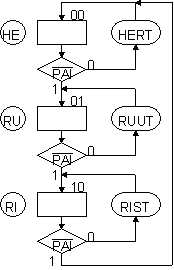
ASM -ja lohkokaavio
|
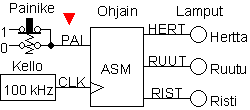
Esimerkin omaisesti tehdään painikesignaalista (PAI) nollassa aktiivinen: haluttu toiminto tapahtuu
silloin, kun PAI saa arvon nolla (ks. lohkokaaviota yllä, painike (PAI)=0 kun sitä painetaan). Valtinarvontakone voidaan toteuttaa kolmitilaisena, kun se tehdään
Mealyn koneena. Mooren kone -toteutuskin voitaisiin tehdä kolmitilaisena. Tällöin kuitenkin lamput
vilkkuisivat (ainakin teoriassa) koko kierron ajan, mikä ei juurikaan olisi järkevää. Toteutetaan
valtinarvontakone erikseen sekä D- että JK -kiikuilla.
Koska koneeseen tulee kolme tilaa, tarvitaan kaksi kiikkua
ja yksi tila jää käyttämättömäksi. (Kahdella kiikulla saadaan 22=4 tilaa)
|
|
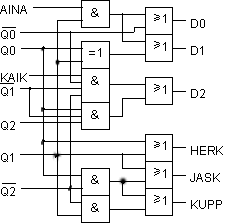
D-kiikkutoteutus
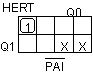 HERT = PAIQ0'Q1' HERT = PAIQ0'Q1'
|
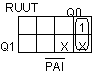 RUUT = PAIQ0 RUUT = PAIQ0
|
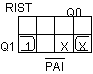 RIST = PAIQ1 RIST = PAIQ1
|
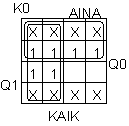
Maija-pelin valtinarvontakoneen JK-kiikkutoteutus
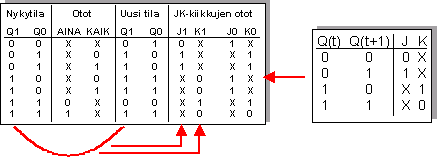
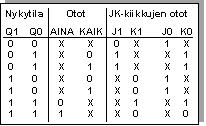
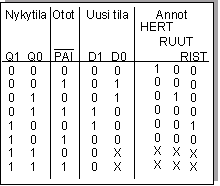
Tilataulu
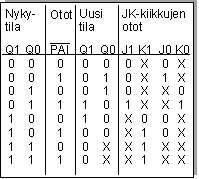
|
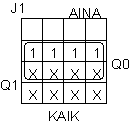
Kiikkujen otot:
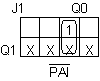 J1 = PAI'Q0
|
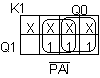 K1 = PAI' + Q0
|
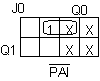 J0 = PAI'Q1'
|
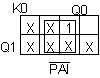 K0 = PAI'
|
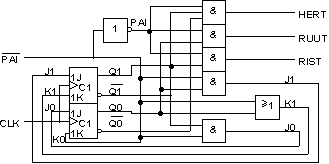
JK-kiikkutoteutuksen antojen lausekkeet ovat samat kuin D-kiikkutoteutuksellakin.
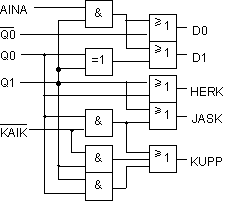
Alla esitetään molempien toteutuksien piirikaaviot. JK -kiikkutoteutuksen on hieman
yksinkertaisempi:
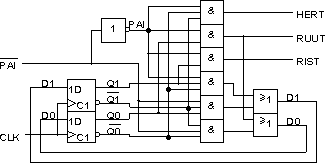
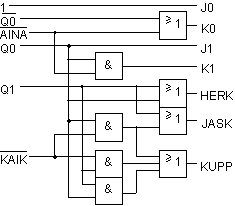
D-kiikkutoteutuksen piirikaavio
|
|
JK-kiikkutoteutuksen piirikaavio
|
Paluu päävalikkoon




















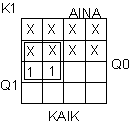


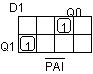 D1 = PAI'Q0Q1' +
PAIQ0'Q1
D1 = PAI'Q0Q1' +
PAIQ0'Q1
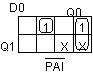 D0 = PAI'Q0'Q1' + PAIQ0
D0 = PAI'Q0'Q1' + PAIQ0
 HERT = PAIQ0'Q1'
HERT = PAIQ0'Q1'
 RUUT = PAIQ0
RUUT = PAIQ0
 RIST = PAIQ1
RIST = PAIQ1






