Signaalinkäsittelytekniikan laboratorio
Digitaalitekniikan perusteet - luento 2
Tietokoneen rakenne
Tietokone on laajasti käytetty apuväline yhteiskunnan eri aloilla. Sen vahvuus on monikäyttöisyys.
(Samalla fyysisellä laitteella pystytään suorittamaan eri tyyppisiä tehtäviä, laitetta voidaan
myös jatkuvasti päivittämään.) Toisaalta suuri osa tietokoneista on erikoistunut suorittamaan tietyn tyyppisiä
tehtäviä. Tietokone on siis digitaalilaite. Sen toiminnan pääpiirteet (huomattavan
yksinkertaistetusti) esitetään alla:
Tietokoneen ydin on integroitu piirielementti, jota kutsutaan prosessoriksi.
Nykyään prosessorit ovat erittäin monimutkaisia ja sisältävät miljoonia transistoreita.
Prosessori suorittaa kaikki koneen toiminnot, jotka ovat kaikki käytännössä erilaisia laskuja,
hyppyjä tai muistihakuja. Sen toiminnan määräävät ohjelmat. Prosessori jakaantuu neljään
toiminnalliseen yksikköön:
- CPU, Central Processing Unit
- sisältää ohjaimen (Control Unit) ja suorittimen (Datapath). Ohjain hakee
muistista käskyjä peräjälkeen ja ohjaa suorittimen toimintaa niiden mukaisesti.
- FPU: Floating-Point Unit
- toimii samantyyppisesti kuin CPU, mutta on erikoistunut ns. liukulukujen
laskutoimituksiin
- MMU: Memory Management Unit
- ohjaa muistin toimintaa
- Internal Cache (suomennos olisi suunnilleen sisäinen lähimuisti)
- Nopeimmin haettava muistiaines sijaitsee täällä. MMU:n ohjaama Internal Cache
sisältää aktiivisimmin tarvittavaa muistiainesta.
(Tulevaisuuden multimediatietokoneissa tämä hierarkinen muistirakenne ei tule toimimaan.
Yksi mahdollisuus on silloin liittää suuri määrä nopeaa DRAM -muistia suoraan prosessorin
yhteyteen.)
Prosessorin lisäksi tietokone sisältää lisää muistia, joka voidaan jakaa kahteen luokkaan:
- ROM, Read Only Memory (suomeksi kiintomuisti): Tämän muistin
muistiaines on pysyvää. Muistista voi lukea, mutta sinne ei voi kirjoittaa.
Käytetään laitteen ohjelman säilytykseen, voi sisältää joitakin vakioarvoja.
- RAM, Random Access Memory (suomeksi vaihtomuisti): Muistista
voi lukea ja sinne voi myös kirjoittaa. Tänne talletetaan ohjelman väli- ja
lopputuloksia sekä erilaista tarvittavaa dataa. RAM-muisti voi olla joko
staattista (SRAM) tai dynaamista (DRAM). RAM-muisti tyhjenee kun tietokoneesta katkaistaan
virta. Lisäksi DRAM vaatii jatkuvaa uudelleen virkistystä, eli muistin sisältö
täytyy määräajoin kirjoittaa uudelleen.
Kaikki muut tietokoneen yksiköt (prosessorin ja muistin lisäksi) voidaan laskea syöttö-
tai tulostuslaitteistoon. (I/O Devices, Input/Output). Näitä ovat esim. näyttö, näppäimistö,
hiiri, erilaiset lisäkortit, tulostin jne.. Kiintolevy voidaan luokitella sekä I/O-välineeksi
että osaksi muistia. Syöttö- ja tulostuslaitteisto on kommunikointirajapinta ulkomaailman kanssa.
(Kansankielellä sanotaan, että kone ottaa tietoja syöttölaitteen välityksellä ja antaa palautteen
tulostuslaitteen kautta. Yleisesti digitaalilaitteessa yhteys ulkomaailmaan hoidetaan otto- ja
antopiirien kautta.)
Tietokoneen eri osia yhdistää väylä (Bus). Väylää pitkin siirretään tiedot yksiköltä toiselle.
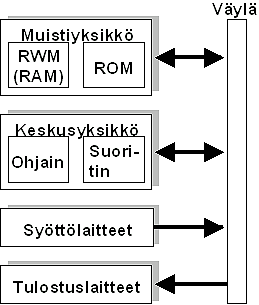
Kaavakuva tietokoneen rakenteesta:
Tässä on yksi vaihtoehto, jolla tietokonetta voidaan kuvata. Kannattaa muistaa, että kuva ei
ole missään suhteessa kattava tai edes ylimalkainen. Lähinnä pyrimme esittelemään yhden
hyvin yksinkertaisen mahdollisuuden jakaa kone toiminnallisiin kokonaisuuksiin. (Lukija voi halutessaan
piirrellä kotonaan yksityiskohtaisemman kaaviokuvan.)
- Muistiyksikössä on ohjelma, lähtötiedot, tulostiedot ja työtiedot
- Keskusyksikkö hakee muistista käskyn ja suorittaa sen, hakee seuraavan
käskyn, suorittaa sen jne..
- Syöttö- ja tulostuslaitteet ovat yhteys ulkomaailmaan: ihmiseen ja ohjattaviin tai
tutkittaviin prosesseihin.
- Väylä on ohjelman (käskyjen) ja tietojen siirtotie tietokoneessa
- Tietokoneen toiminta on pääasiassa sarjamuotoista mutta nopeaa.
|
|
Lisää tietokoneen rakenteesta ja toimintamalleista kerrotaan tietotekniikan osaston kurssilla Tietokoneen arkkitehtuuri.
Lukujärjestelmistä
Nykyinen kymmenjärjestelmämme on perua hedelmällisen puolikuun alueelta ja se on syntynyt jonkin
verran ennen ajanlaskumme alkua. Kymmenjärjestelmä perustuu nimensä mukaisesti luvun kymmenen
eri potensseihin. Käytetyt numeroarvot ovat 0,1,2,3,4,5,6,7, 8, 9.
Kymmenjärjestelmä voidaan tulkita muodossa:
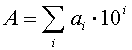
, missä ai on jokin kerroin välitä [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Esimerkiksi luku 3025 tarkoittaa oikeastaan lauseketta 3 × 103 + 0 ×
102 + 2 × 101 + 5 × 100.
Toisena esimerkkinä luku 1978, joka tarkoittaa samaa kuin lauseke 1 × 103 + 9 ×
102 + 7 × 101 + 8 × 100.
Eli ensin tuhannet, sitten sadat, kymmenet ja lopuksi ykköset.
Edellä kuvatun ymmärtäminen on tärkeää, jotta voidaan laskea yhteyksiä lukujärjestelmistä
toisiin. 10 (eli desimaali) -järjestelmä ei ole läheskään ainoa mahdollinen. Muita paljon
käytettyjä ovat erityisesti digitaalilogiikassa käytetty 2-kantajärjestelmä (binääri),
8-kantajärjestelmä (oktaali) ja 16-kantajärjestelmä (heksadesimaali).
Alla olevasta taulukosta nähdään eri lukujärjestelmien vastaavuuksia:
| Heksadesimaali | Desimaali | Oktaali | Binääri |
|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| A | 10 | 12 | 1010 |
| B | 11 | 13 | 1011 |
| C | 12 | 14 | 1100 |
| D | 13 | 15 | 1101 |
| E | 14 | 16 | 1110 |
| F | 15 | 17 | 1111 |
Taulukosta nähdään, että numeroita minimoidakseen kannattaa käyttää mahdollisimman
suurikantaista järjestelmää: siinä missä heksadesimaalijärjestelmässä selvitään yhdellä
numerolla joudutaan binäärijärjestelmässä pahimmillaan käyttämään neljää numeroa ilmaisemaan
samaa lukua. Binäärijärjestelmän laskutoimitukset ovat kuitenkin niin yksinkertaisia, että
se on monissa tilanteissa kannattavin vaihtoehto.
Ihmiselle luontevin näyttää olevan desimaalijärjestelmä. Laitteissa taas tarkoituksesta
riippuen yleensä kannattaa käyttää jotain muuta järjestelmää. (Lähes aina binäärijärjestelmää
tai sen monikertaa oktaali- tai heksadesimaalijärjestelmää.) Silloin tulostus- ja syöttölaitteita varten tarvitaan muunnoksia
lukujärjestelmästä toiseen.
Hyvän digitaalisuunnittelijan tulisi osata perusteellisesti binääri-, oktaali- ja heksadesimaalijärjestelmien
väliset suhteet. Samoin tulisi osata nopeasti ratkaista, mitä tietty kymmenjärjestelmän luku on näissä kolmessa
järjestelmässä. Lukujärjestelmämuunnoksia esitellään tarkemmin seuraavilla sivuilla.
Lukujärjestelmämuunnokset
Muusta järjestelmästä desimaalijärjestelmään
Lukujärjestelmästä toiseen siirtyminen vaatii laskemista. Jos otetaan perusjärjestelmäksi
tuttu desimaalijärjestelmä, muista siihen siirtyminen on helppoa. Lausekemuotoinen määrittely
mille tahansa järjestelmälle suhteessa kymmenjärjestelmään voitaisiin ilmaista vaikka
seuraavasti:
Luku = Summai ( kerroini × kantalukui )
Kun siirrytään jostain muusta järjestelmästä kymmenjärjestelmään, voidaan soveltaa kaavaa
suoraan.
Esim. luku (2634)7 (eli luku 2634 7-kantajärjestelmässä) voidaan laskea suoraan
auki seuraavasti:
(2634)7 = 2 × 73 + 6 × 72 + 3 ×
71 + 4 × 70
= 686 + 294 + 21 + 4 = (1005)10
Tässä kantaluku on tietystikin 7, sillä muunnettavaluku on 7-kantajärjestelmässä.
Kaavassa potenssit tulevat sen mukaan millä kohtaa kyseinen numero on alkuperäisessä luvussa (2634)7 eli tuhannet saavat potenssiluvun 3, sadat saavat potenssiluvun 2 jne.
Desimaalijärjestelmästä muuhun järjestelmään
Kun halutaan siirtää luku (n) toiseen suuntaan, etsitään suurinta halutun kantaluvun (k)
potenssia (i), joka 'mahtuu' siirrettävään lukuun. (Eli n ÷ ki yhtäsuuri
tai suurempi kuin 1) Kun suurin mahdollinen potenssi löydetään, suoritetaan jakolasku N ÷
ki ja siirrytään tarkastelemaan mahdollista jakojäännöstä.
Eli:
- Etsitään uuden kantaluvun (k) suurin potenssi (i), joka mahtuu 10-järjestelmän lukuun.
- Lasketaan, montako kertaa kyseinen potenssi mahtuu alkuperäiseen lukuun, kerroin
on uuden luvun eniten merkitsevä numero.
- Lasketaan jakojäännös yhtälöstä vanhaluku - (kerroin × kantalukupotenssi)
ja tarkastellaan sitä.
- Etsitään uuden kantaluvun potenssi, joka mahtuu jakojäännökseen.
- Lasketaan, montako kertaa tämä potenssi mahtuu jakojäännökseen, saatava kerroin on uuden
luvun seuraavaksi eniten merkitsevä numero.
- Lasketaan jälleen uusi osamäärä, tarkastellaan sitä jne.. kunnes koko luku on käyty läpi.
- Uusi luku muodostuu kertoimista.
Esimerkki lukujärjestelmämuunnoksesta:
Muunnetaan luku (3718)10 7-kantajärjestelmään.
- Etsitään iteroimalla/kokeilemalla 7:n (haluttu kantaluku) suurin potenssi, joka mahtuu kyseiseen vanhaan 10-järjestelmän lukuun:
74 = 2401 < 3718 < 75 = 16807
- 74 mahtuu lukuun 3718 yhden kerran (3718 ÷ 74 = 1,548521), joten uuden luvun eniten merkitseväksi kertoimeksi tulee 1
- Tarkastellaan jakolaskun jäännöstä ( = 3718 - 1 × 74 = 1317):
- 73 = 343 < 1317 < 74 = 2401
- 73 mahtuu jakojäännökseen 3 kertaa (1317 ÷ 73 = 3,83965) joten uuden luvun toiseksi suurimmaksi kertoimeksi tulee 3
- lasketaan seuraava jakojäännös: 1317 - 3 × 73 = 288
72 = 49 < 288 < 73 = 343
72 mahtuu 288:n 5 kertaa (288 ÷ 72 = 5,87755), joten uuden luvun seuraavaksi kertoimeksi tulee 5
lasketaan seuraava jakojäännös: 288 - 5 × 72 = 43
71 = 7 < 43 < 72 = 49
71 mahtuu 43:een 6 kertaa (43 ÷ 71 = 6,142857), joten uuden luvun seuraavaksi kertoimeksi tulee 6
lasketaan seuraava jakojäännös: 43 - 6 × 71 = 1
osamääräksi jää 1, joka on suoraan uuden luvun viimeinen numero
- uusi luku on siis (13561)7
Esimerkki 2.
Muunnetaan luku (1241)10 5-kantajärjestelmään.
- Etsitään iteroimalla/kokeilemalla 5:n (haluttu kantaluku) suurin potenssi, joka mahtuu kyseiseen vanhaan 10-järjestelmän lukuun:
54 = 625 < 1241 < 55 = 3125
- 54 mahtuu lukuun 1241 yhden kerran (1241 ÷ 54 = 1,9856), joten uuden luvun eniten merkitseväksi kertoimeksi tulee 1
- Tarkastellaan jakolaskun jäännöstä ( = 1241 - 1 × 54 = 616):
- 53 = 125 < 616 < 54 = 625
- 53 mahtuu jakojäännökseen 4 kertaa (616 ÷ 53 = 4,928) joten uuden luvun toiseksi suurimmaksi kertoimeksi tulee 4
- lasketaan seuraava jakojäännös: 616 - 4 × 53 = 116
52 = 25 < 116 < 53 = 125
52 mahtuu 116:n 4 kertaa (116 ÷ 52 = 4,64), joten uuden luvun seuraavaksi kertoimeksi tulee 4
lasketaan seuraava jakojäännös: 116 - 4 × 52 = 16
51 = 5 < 16 < 52 = 25
51 mahtuu 16:een 3 kertaa (16 ÷ 51 = 3,2), joten uuden luvun seuraavaksi kertoimeksi tulee 3
lasketaan seuraava jakojäännös: 16 - 3 × 51 = 1
osamääräksi jää 1, joka on suoraan uuden luvun viimeinen numero
- uusi luku on siis (14431)5
Tulos voidaan vielä varmistaa jo aiemmin opitun muunnoksen avulla (5-järj. --> 10-järj.)
Saadaan seuraavaa:
(14431)
5 = 1 × 5
4 + 4 × 5
3 + 4 ×
5
2 + 3 × 5
1 + + 1 × 5
0
= 625 + 500 + 100 + 15 + 1 = (1241)
10
Huom: Ylläolevat periaatteet soveltuvat etumerkki-itseisarvomuotoisten
(=jo peruskoulussa opittu 'tavallinen' tapa esittää positiivisia ja negatiivisia lukuja)
kokonaislukujen muuntamiseen järjestelmästä toiseen. Oma lukunsa on desimaalilukujen tai
komplementoitujen (toinen tapa esittää etumerkillisiä lukuja) lukujen muuntaminen.
Binääriluvuista
Digitaalilogiikassa yleisimmin käytetään binääri- eli kaksikantajärjestelmää. Järjestelmän
pienin erillinen yksikkö on bitti. Bitillä voi olla kaksi arvoa, 1 tai 0. Binäärilukujen
vahvuuksia ovat laskutoimitusten yksinkertaisuudet ja lukujen fysikaalisen esittämisen
helppous. (On vain kaksi numeroa.) Heikkouksia ovat lukujen pituudet, epähavainnollisuus
ja laskutoimituksien suuri määrä. Digitaalilaitteissa binäärilukuja säilytetään rekistereissä.
Luvun esittämiseen on käytössä tietty vakiomäärä tai sen monikerta bittejä. Esimerkiksi
8, 16 tai 32.
Esimerkki 2-kantajärjestelmän luvusta: 0110102 = 1 × 2 4 + 1
× 2 3 + 1 × 2 1 = 26 10.
2. Esimerkki 2-kantajärjestelmän luvusta: 1010012 = 1 × 2 5 + 1
× 2 3 + 1 × 2 0 = 41 10.
Ylläolevan esimerkin lukua sanotaan kiinteän pilkun luvuksi. Kiinteän pilkun luvut ovat aina
kokonaislukuja. Ne voivat olla joko positiivisia lukuja, jolloin luku tulkitaan sellaisenaan tai
etumerkillisiä. Tällöin luvun eniten merkitsevä bitti
on merkkibitti. Yleensä 1 tarkoittaa miinusta ja 0 plussaa.
Etumerkillisillä luvuilla on erilaisia esitystapoja:
- Etumerkki-itseisarvoesitys: esitys toimii kuten desimaaliluvuissa ollaan totuttu.
Tämä esitys hankaloittaa yhteen- ja vähennyslaskua, kertolasku on yksinkertainen. Etumerkki-itseisarvoesityksessä
eniten merkitsevä bitti on siis etumerkkibitti, loput bitit muodostavat varsinaisen luvun.
Ensimmäistä bittiä ei oteta huomioon luvun arvoa laskettaessa, muut bitit tulkitaan normaalisti.
Esimerkiksi 4-bittinen luku 10102. Tässä ensimmäinen bitti on merkkibitti, joka kertoo
luvun olevan negatiivinen,
koska merkkibitti on 1. Loput bitit (010) kertovat, että luvun itseisarvo on 2 (1 × 2 1 = 2).
Näin 10102 = - (0 × 2 2 + 1 × 2 1 + 0 × 2 0) = -210
2. Esimerkki 5-bittinen luku 110012. Tässä ensimmäinen bitti on jälleen merkkibitti, joka kertoo
luvun olevan negatiivinen,
koska merkkibitti on 1. Loput bitit (1001) kertovat, että luvun itseisarvo on 9 (1 × 2 3 + 1 × 2 0 = 9).
Näin 110012 = - (1 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0) = -910
- BCD (Binary Coded Decimal) -luvut ovat 10-järjestelmän lukuja joiden jokainen numero on muutettu erikseen binääriseksi
Esimerkiksi 10-järjestelmän luku 2410 saadaan BCD-muotoon muuttamalla erikseen binääriseksi luvut 2 ja 4.
Muuntaminen binääriseksi tapahtuu samalla tavalla kuin mihin tahansa kantaan (binääriluvuthan ovat 2-kantajärjestelmän lukuja)
210 --> 102
410 --> 1002
Kaikki BCD luvut esitetään lopulta neljällä bitillä, koska suurin numero joka voidaan joutua muuttamaan on 910, joka on binäärijärjestelmässä 1001 ts.
2410 --> 0010 0100 (BCD)
2. Esimerkki 10-järjestelmän luku 16510 esitettynä BCD-muodossa saadaan kun kaikki kolme numeroa muutetaan erikseen binääriseksi.
110 --> 12
610 --> 1102
510 --> 1012
Ja kun kaikki BCD luvut esitetään lopulta neljällä bitillä saadaan
16510 --> 0001 0110 0101 (BCD)
- 1-komplementtimuoto (tämä on melko harvinainen, yhteen- ja vähennyslaskuoperaatiot
ovat suhteellisen yksinkertaisia)
- 2- komplementtimuoto (yleisin tapa esittää lukuja digitaalilaitteissa, yhteen- ja
vähennyslaskualgoritmit ovat erittäin yksinkertaisia)
Alla olevasta taulukosta binääriluvun esittäminen eri esitystavoissa:
Desimaali
luku | Etumerkki
-itseisarvo | 1:n
komplementti | 2:n
komplementti |
|---|
| +7 | 0111 | 0111 | 0111 |
| +6 | 0110 | 0110 | 0110 |
| +5 | 0101 | 0101 | 0101 |
| +4 | 0100 | 0100 | 0100 |
| +3 | 0011 | 0011 | 0011 |
| +2 | 0010 | 0010 | 0010 |
| +1 | 0001 | 0001 | 0001 |
| +0 | 0000 | 0000 | 0000 |
| -0 | 1000 | 1111 | -- |
| -1 | 1001 | 1110 | 1111 |
| -2 | 1010 | 1101 | 1110 |
| -3 | 1011 | 1100 | 1101 |
| -4 | 1100 | 1011 | 1100 |
| -5 | 1101 | 1010 | 1011 |
| -6 | 1110 | 1001 | 1010 |
| -7 | 1111 | 1000 | 1001 |
| -8 | -- | -- | 1000 |
Kiinteän pilkun luvut ovat siis aina kokonaislukuja. Desimaalilukujen sekä hyvin suurten tai hyvin pienten
lukujen esittämiseen käytetään liukuvan pilkun lukuja. Liukuvan pilkun luku jakaantuu kolmeen osaan: merkkibittiin,
eksponenttiin ja mantissaan.
Esim seuraavasti (kyseessä on 32-bittinen liukuvan pilkun luku):
| s | e | e | e | e | e | e | e | e | f | f |
f | f | f | f | f | f | f | f |
f | f | f | f | f | f | f | f | f |
f | f | f | f |
s = merkkibitti (aina 1 kpl)
e = eksponentin bitit (tässä tapauksessa 8 kpl)
f = mantissan bitit (tässä tapauksessa 23 kpl)
On siis sovittu, että kyseisessä bittijonossa ensimmäinen bitti kertoo luvun etumerkin. Siitä tietty määrä seuraavia bittejä
ilmaisee luvun kantaluvun eksponentin arvon. Loput bitit tulkitaan mantissana. Liukuluvuista on olemassa muutama eri standardi.
Tässä materiaalissa esitetään niistä yksi. Liukuluvun laskentakaava on esitetty alla:
Luku = (-1)s × 2e × 1.f
(Liukuluvuista lisää myöhemmin.)
Binäärijärjestelmän komplementeista
Yleisesti missä tahansa lukujärjestelmässä (kantaluku r), on kaksi erityyppistä komplementtia:
kantaluvun komplementti (radix complement) ja kantaluvun heikennetty komplementti
(diminished radix complement). Näistä edellistä kutsutaan r:n (eli kantaluvun) komplementiksi
ja jälkimmäistä (r -1 ):n komplementiksi. Nämä komplementit binäärijärjestelmän tapauksessa
ovat siis 2:n komplementti ja 1:n komplementti, sillä binäärijärjestelmän kantalukuhan on 2.
Komplementtia tarvitaan digitaalijärjestelmissä kuvaamaan negatiivisia ja positiivisia lukuja. Komplementointi on eräänlaista
lukualueen peilaamista tietyn peilauskohdan suhteen. Kyseessä on taas sopimus: on sovittu, että tiettyä rajapyykkiä itseisarvoltaan
suuremmat binäärisarjat tulkitaan negatiivisina ja tätä samaa rajapyykkiä pienemmät positiivisina. Rajapyykki sijoitetaan mahdollisimman
tarkasti lukualueen puoliväliin.
Käytäntö on, että jos komplementtiluvun eniten merkitsevä bitti on 0, luku on
positiivinen. Jos komplementtiluvun eniten merkitsevä bitti on 1, on luku negatiivinen.
Jos luku on positiivinen, se tulkitaan
normaalisti sijoittamalla lausekkeeseen tarvittavat kakkosen kantaluvut, kuten on aiemminkin jo tehty.
(Esim 0101 = 1 × 2 2
+ 1 × 2 0 = 4 + 1 = 5).
Jos luku on negatiivinen, täytyy tehdä
peilausoperaatio. Peilauksessa (riippuen komplementin tyypistä) suhteutetaan loput bittisarjan bitit ensimmäiseen lukuun.
Esimerkiksi luku 10101. Eniten merkitsevä bitti on 1, joten luvun muut bitit peilataan sen suhteen.2-komplementin tapauksessa peilaus tapahtuu näin: 10101 = -16 + 4 + 1 = -11.
(Jos komplementin idea ei heti aukea, ei kannata masentua. Normaalielämässä riittää pitkälle, jos muistaa, että komplementointi
tarkoittaa lukualueen peilausta. Digitaalisuunnittelussa työkalut yleensä huolehtivat komplementoinnista.
Siihen törmätään vain erityisen haastavissa tapauksissa tai ongelmatilanteissa. Tentissä tosin asiaa kysytään usein jonkin verran.)
1-komplementti
Olkoon B positiivinen kokonaisluku, jonka suuruusosan esityspituus on n bittiä.
Tällöin B:n 1:n komplementti on
C1,n (B) = 2n - 1 - B
1-komplementin muuntaminen desimaalimuotoon kannattaa tehdä siten, että muunnetaan luku ensin
2-komplementtiin. Komplementtien välillä vallitsee yhteys:
C2,n(B) = C1,n(B) + 1
2-komplementti
Olkoon B positiivinen kokonaisluku, jonka suuruusosan esityspituus on n bittiä.
Tällöin B:n 2:n komplementti on
C2,n(B) = 2n - B
Käytännössä helppona nyrkkisääntönä voidaan muistaa seuraavaa: Jos luku on positiivinen,
se tulkitaan normaalisti. Tällöin muunnos 10-järjestelmään tapahtuu aivan samalla tavalla kuin on aiemmin esitetty.
Jos luku on negatiivinen, tulkitaan luvun eniten merkitsevä bitti
(merkkibitti) aivan kuin se olisi tavallinen kerroin, mutta negatiivisena. Tämän jälkeen tulkitaan
muut kertoimet positiivisina.
Esimerkki 1
Luku 1001102 (luku on siis 2-komplementtimuodossa, merkkibitti on 1 eli luku on
negatiivinen) tulkitaan seuraavasti:
1001102 = -1 × 25 +
1 × 22 + 1 × 21 = -3210 + 410 + 210 = -2610
Esimerkki 2
Luku 1011012 (luku on siis 2-komplementtimuodossa, merkkibitti on 1 eli luku on
negatiivinen) tulkitaan seuraavasti:
1011012 = -1 × 25 +
1 × 23 + 1 × 22 + 1 × 20 = -3210 + 810 + 410 + 110= -1910
Esimerkki 3
Luku 0110012 (luku on siis 2-komplementtimuodossa, merkkibitti on 0 eli luku on
positiivinen) tulkitaan seuraavasti:
0110012 = 1 × 24 +
1 × 23 + 1 × 20 = 1610 + 810 + 110 = 2510
Binääriluvun komplementin muodostaminen
1-komplementti on helppo muodostaa:
Kaavaa ( C1,n (B) = 2n - 1 - B ) tulkittaessa huomataan, että 1-komplementin
luvusta saa suoraan kääntämällä kaikki bitit nurin (eli ykkösestä tulee nolla, nollasta ykkönen).
Jos luku on lyhyempi kuin käytetty bittien määrä, lisätään alkuun lisää nollia ja käännetään ne
muunnoksessa ykkösiksi. Eli esim. jos on valittu 4 bittinen esitys tapa ja käsiteltävä luku on 510 = 1012. Nyt pitää lisätä yksi nolla luvun alkuun jolloin luvuksi tulee 01012
HUOM ! Mikäli luku on aluksi itseisarvo-etumerkki muodossa, jätetään etumerkki rauhaan. Siis etumerkkiä ei käännetä edellisen ohjeen mukaisesti vaan se pysyy samana.
Esimerkki 1
Suuruusosan esityspituus 7 bittiä, luku B=11001 (=2510)
- Lisätään tarvittavat nollat: B=0011001
- Käännetään bitit: C1,7(B) = 1100110, mikä on haluttu tulos
Tuloksen voi tarkistaa muuntamalla sen edelleen 2-komplementiksi ja sitä kautta kymmenjärjestelmään:
2-komplementiksi eli lisätään 1: C2,7(B)=1100111=
Muuntaminen 2-komplementista 10-järjestelmään tehdään kuten on esitetty edellä:
C2,7(B)=1100111= -26 + 25 +
22 + 21 + 20 = -2510
Esimerkki 2
0110011
Suuruusosan esityspituus 7 bittiä, luku B=1001101 (=7710)
- Nyt ei tarvitse lisätä numeroita luvun eteen, sillä sen pituus on jo 7 bittiä.
- Käännetään bitit: C1,7(B) = 0110010, mikä on haluttu tulos
Tuloksen voi tarkistaa muuntamalla sen edelleen 2-komplementiksi ja sitä kautta kymmenjärjestelmään:
2-komplementiksi eli lisätään 1: C2,7(B)=0110011.
HUOM ! Tämä vaikuttaisi olevan positiivinen luku, mutta sehän ei voi olla sitä, koska
edellä suoritimme komplementtia muodostaessamme peilauksen. Tämän takia tulee nyt lisätä yksi ykkönen koko luvun eteen, jotta tulos olis negatiivinen kuten pitääkin.
C2,7(B)=10110011= -27 + 25 +
24 + 21 + 20= -7710
Esimerkki 3
Suuruusosan esityspituus 7 bittiä, luku (itseisarvo-etumerkki muodossa) B=10011010 (=-2610). Ensimmäinen bitti kertoo etumerkin (1 = -)ja sitten tulee luvun suuruusosa (7 bittiä).
- Nyt ei kosketa lainkaan etumerkkiin. Lisäksi huomataan, että suuruusosa on jo 7 bittiä pitkä, joten ei tarvetta toimenpiteisiin.
- Käännetään bitit: C1,7(B) = 11100101, mikä on haluttu tulos
Tuloksen voi tarkistaa muuntamalla sen edelleen 2-komplementiksi ja sitä kautta kymmenjärjestelmään:
2-komplementiksi eli lisätään 1: C2,7(B)=11100110= -27 + 26 +
+ 25 + 22 + 21 = -2610
Esimerkki 4
Suuruusosan esityspituus 7 bittiä, luku (itseisarvo-etumerkki muotoinen) B=11001 (=-910). Ensimmäinen bitti kertoo etumerkin ( 1 = -)ja sitten tulee luvun suuruusosa (4 bittiä).
- Nyt ei taaskaan kosketa lainkaan etumerkkiin. Huomataan kuitenkin, että suuruusosa on vain 4 bittiä pitkä, joten siihen lisätään nollia. Näin saadaan:
B=10001001, missä lisätyt nollat on lihavoitu.
- Lopuksi käännetään bitit: C1,7(B) = 11110110, mikä on haluttu tulos
Tuloksen voi tarkistaa muuntamalla sen edelleen 2-komplementiksi ja sitä kautta kymmenjärjestelmään:
2-komplementiksi eli lisätään 1: C2,7(B)=11110111= -27 + 26 +
25 + 24 + 22 + 21 + 20 = -910
Esimerkki 5
Suuruusosan esityspituus 7 bittiä, luku (itseisarvo-etumerkki muotoinen) B=01100 (=1210). Ensimmäinen bitti kertoo etumerkin (0 = +)ja sitten tulee luvun suuruusosa (4 bittiä).
- Nyt ei taaskaan kosketa lainkaan etumerkkiin. Huomataan kuitenkin, että suuruusosa on vain 4 bittiä pitkä, joten siihen lisätään nollia. Näin saadaan:
B=00001100, missä lisätyt nollat on lihavoitu.
- Lopuksi käännetään bitit: C1,7(B) = 00001100, mikä on haluttu tulos
HUOM! Tässä oli siis positiivisen luvun muuntaminen 1-komplementtiin. Tarkkasilmäisimmät voivat huomata, että luku ei muuttunut lainkaan (mitä nyt nollia tuli lisää..) Jos tämä tuntuu hämärältä ks. selitystä aiemmin komplementin johdannon kohdalta.
Tuloksen voi tarkistaa muuntamalla sen edelleen 2-komplementiksi ja sitä kautta kymmenjärjestelmään:
Muuntaminen 2-komplementiksi on helppoa positiivisen luvun tapauksessa. Ei tehdä mitään muutoksia eli: C2,7(B)=00001100= 23 + 22
= 1210
2-komplementti muodostetaan joko 1-komplementin kautta lisäämällä siihen 1
(kuten edellisen esimerkin tarkistusosassa) tai suoraan seuraavalla algoritmillä:
- aloitetaan vähiten merkitsevästä bitistä
- jos bitti on 0 sitä ei muuteta, vaan siirrytään seuraavaan
- ensimmäinen vastaantuleva 1-bitti säilytetään ennallaan
- loput bitit käännetään (kaikki)
Esimerkki
Suuruusosan esityspituus 7 bittiä, luku B=10100= 0010100 ( = 10 10 )
C2,7(B)=1101100 ( = -10 10 )
Komplementin komplementti
C2,n(C2,n(B))= 2n - (2n - B) = B
C1,n(C1,n(B))= 2n - 1 - (2n - 1 - B) = B
Komplementoimalla komplementti saadaan siis alkuperäinen luku uudelleen.
Pari esimerkkimuunnosta
| |
Etumerkki-itseisarvoinen luku |
1:n komplementti |
2:n komplementti |
| A | 01100011 | 01100011 | 01100011 |
| B | 10110010 | 11001101 | 11001110 |
Positiiviset luvut ovat siis joka muodossa samanlaisia. Negatiivisissa suuruusosasta
tehdään komplementti. Etumerkki (jos sellainen on) jätetään komplementoitaessa rauhaan.
Muiden lukujärjestelmien komplementeista
Komplementti voidaan ottaa myös muissa lukujärjestelmissä kuin binäärijärjestelmässä. Tässä on esitetty esimerkinomaisesti miten
tapahtuu muuntaminen muissa lukujärjestelmissä. Mikäli etumerkki sisältyy ensimmäiseen lukuun, se on komplementtimuodossa.
Esimerkki 1
Luku +378 (=3110) on itseisarvo-etumerkki muodossa.
- Muistetaan, että komplementoitaessa positiivista lukua ei luvulle tapahdu mitään. Näin ollen:
+378 komplementoituna on 378
Tuloksen voi tarkistaa muuntamalla sen takaisin 10-järjestelmään:
378 = 3 × 81 + 7 × 80 = 24 + 7 = 3110
Esimerkki 2
Luku -214 (=-910) on itseisarvo-etumerkki muodossa.
- Nyt negatiivisen luvun komplementoinnissa on syytä olla tarkkana !
- Ensinnäkin huomataan, että suurin mahdollinen luku 4-järjestelmässä kahdella numerolla esitettynä on 334. Tämä vastaa lukua -110 komplementoinnin takia.
Kun luvun ensimmäinen numero on 0 tai 1 = (+) on kyseessä positiivinen luku ja kun ensimmäinen numero on 2 tai 3 = (-), on kyseessä negatiivinen luku. Näin ollen:
Nyt tiedetään, että tulokseksi on tulossa negatiivinen luku ts. komplementoidun luvun ensimmäinen numero on 2 tai 3
Lasketaan 334-214+14 = 134 Tämä on väärin! Ensimmäinen numero osoittaisi luvun olevan positiivinen, mitä se ei ole!!
Tarvitsemme siis esitystä kolmella numerolla jolloin luku 3334 = -110
Lasketaan 3334-214+14 = 3134
Tämä on haluttu vastaus.
Hieman lisäselvitystä
- Suurin luku 4-järjestelmässä on kahdella numerolla 33 tai kolmella 333. Vastaavasti 9-järjestelmässä 88 tai 888.
Tämä suurin luku vastaa lukua -110, mikäli ei olla itseisarvo-etumerkki-esityksessä. (Tällöinhän luvun etumerkin ilmoittaa suoraan + tai -)
- Pienin negatiivinen luku olisi esimerkin tapauksessa 2004 = -3210
- Se miksi laskutoimituksissa on mukana +1 johtuu siitä, että aloitamme vähennyslaskun laskemisen luvusta -110, emmekä luvusta 010
Toisin sanoen, mikäli emme lisäisi lukua +1, olisi edellinen muunnos ollut luvusta -224
- Luku +1 voidaan myös jättää lisäämättä, mutta silloin täytyy muistaa tietenkin vähentää vain -204 (Esimerkkimme tapauksessa)
Tuloksen voi tarkistaa muuntamalla sen takaisin 10-järjestelmään:
-(3334-3134+14) = -(21)4 = -(2 × 41 + 1 × 40) = - (8 + 1) = -910
Esimerkki 3
Muunnettava luku 1A11 takaisin 10-järjestelmään.
- Luvussa ei näy etumerkkiä, joten tulkitaan se positiiviseksi luvuksi ensimmäisen numeron perusteella.(0-->5 = + ja 6-->A = -)
- Nyt muuntaminen käy helposti, koska luku on positiivinen. Muunnetaan se aivan normaalisti (Komplementtiesityksessähän positiiviset luvut säilyvät muuttumattomina)
- 1 × 111 + 10 × 110 = (11 + 10) = 2110
Hieman lisäselvitystä
- Luku A11 vastaa lukua 1010. Muita kirjaimia kuin A ? ---> Ks. taulukko aiemmin, jossa oli esitelty mm. heksadesimaaliluvut, oktaaliluvut ja desimaaliluvut.
Taulukon löydät lukujärjestelmä osion alusta.
Esimerkki 4
Muunnettava 9-järjestelmän 9-komplementin luku 829 takaisin 10-järjestelmään.
- Luku on negatiivinen ensimmäisen numeron perusteella (0-->4 = + ja 5-->8 = -)
- Nyt mietitään mikä on suurin mahdollinen luku (kahdella numerolla, koska tehtävänantokin oli kahdella numerolla) 9-järjestelmässä.
- Suurin mahdollinen luku on 889 = -110
- Nyt tehdään laskutoimitus: 889 - 829 = 69
69 + 19 = 79
- Lopuksi muunnetaan 79 10-järjestelmään kuten on aiemmin opittu ja muistetaan vielä, että käsitellään negatiivista lukua.
Tulokseksi saadaan : -710
Hieman lisäselvitystä
- Miksi laskutoimituksessa lisätään yksi "ylimääräinen" ykkönen?
Tämä tehdään siksi, että jos olisi seuraavanlainen tilanne: Pitäisi muuntaa luku 889 takaisin
10-järjestelmään. Tällöin muunnos 889-889 = 010. Tämä antaisi tulokseksi luvun nolla. Kuitenkin on sovittu, että 889 vastaa lukua -110. Tämän takia vähennetään yksi "ylimääräinen" ykkönen.
Tämä tapahtuu laskemalla 09 + 19 = 19 , joka muunnetaan 10-järjestelmään muistaen kuitenkin, että kyse on neg.luvusta 19 ==> -110. Tämä on haluttu (ja oikea) lopputulos
Kiinteän pilkun lukujen laskutoimituksia
Etumerkki-itseisarvomuotoisten binäärilukujen yhteenlasku (ja vähennyslasku)
Algoritmi:
- jos merkkibitit ovat samat
- lasketaan suuruusosat yhteen
- merkkibitti säilyy samana
- jos merkkibitit ovat erilaisia
- vähennetään suuruusosaltaan pienempi suuruusosaltaan suuremmasta
- merkkibitti on sama kuin suuruusosaltaan suuremmalla
Esimerkkejä: (Ensimmäinen bitti on merkkibitti 0='+' 1='-')
| A | B | C | D |
|---|
0110 1001
+ 0001 0110 | 1000 1111
+ 0001 0110 | 0100 0110
+ 0011 0011 | 0010 1100
+ 1000 0110 |
|
0111 1111 | 0000 0111 | 0111 1001 | 0010 0110 |
| OK | Merkkibitit
erilaisia! | Muista!
01+01=10 | Merkkibitit
erilaisia! |
B-kohdassa merkkibitit ovat erilaisia, joten vähennetään suuruusosaltaan pienempi (ylempi luku) suuruusosaltaan suuremmasta:
22
10 - 15
10 = 7
10
Vastaava tapaus myös D-kohdassa:
44
10 - 6
10 = 38
10
Jokainen voi itse tarkistaa laskut, esim. muuntamalla ne 10-järjestelmään ja sieltä tulos takaisin binääriseksi.
Binäärilukujen yhteenlaskua varten käytetään kokosummain rakennetta, joka tulee kurssilla myöhemmin esille (luennossa 6).
1-komplementtimuotoisten binäärilukujen yhteenlasku
Algoritmi:
- lasketaan luvut merkkibitteineen yhteen
- jos merkkibiteistä muodostuu ylimääräinen summabitti, lisätään se summan vähiten
merkitsevään bittiin.
Esimerkkejä:
| A | B | C | D |
|---|
0011 0101
+0010 0010 | 1000 1111
+ 0001 0110 |
1011 0010
+0111 0001 | 1111 0111
+1000 0110 |
| 0101 0111 | 1010 0101 | 1 0010 0011
'---------->1
0010 0100 |
10111 1101 |
Muista!
1+1=10 | Muista!
1+1+1=11 | OK | Ylivuoto |
A ja B kohdassa bitit on yksinkertaisesti laskettu yhteen.
C-kohdassa ylimääräinen merkkibitti on lisätty vähiten merkitsevään bittiin.
D-kohdassa tapahtuu ylivuoto (merkkibitti on vaihtunut, luku on liian suuri lukualueeseen. Ks. 2-komplementtien yhteenlaskua).
2-komplementtimuotoisten binäärilukujen yhteenlasku
Algoritmi:
- lasketaan luvut merkkibitteineen yhteen
- poistetaan tarvittaessa merkkibiteistä muodostunut 'ylimääräinen bitti', niin sanottu ylivuoto
Esimerkkejä:
| A | B | C | D |
|---|
0011 0101
+0010 0010 | 1000 1111
+ 0001 0110 |
1011 0010
+0111 0001 | 1111 0111
+1000 0110 |
|
0101 0111 | 1010 0101 | 1 0010 0011
=> 0010 0011 | 1 0111 1101
=>0111 1101 |
| OK | OK | Poistetaan
'ylimääräinen'
bitti | Ylivuoto |
A ja B kohdassa bitit on yksinkertaisesti laskettu yhteen.
C-kohdassa laskuun tulisi ylimääräinen merkkibitti, mutta sitä ei oteta huomioon vaan tiputetaan pois. (Se siis ei näy
lopullisessa tuloksessa.)
D-kohdassa merkkibitti on muuttunut positiiviseksi, vaikka molemmat luvut ovat negatiivisia. Kyseessä on ylivuoto: tulos on itseisarvoltaan liian suuri esitettäväksi
8 bitillä ja näin ollen tulos on siis virheellinen. Tämä on tyypillinen vikatilanne, joka voidaan tavanomaisissa tapauksissa helposti
korjata kasvattamalla sanapituutta eli lisäämällä lukujen esittämiseen käytettävien bittien määrää.
Komplementtimuotoisten lukujen vähennyslasku
- Tehdään vastaluvun yhteenlaskuna: A - B = A + (-B)
- -B = kompl(B)
Komplementtimuotoisten binäärilukujen vähennyslaskuesimerkkejä
A, B, C ja D ovat 2-komplementtimuotoisia binäärilukuja.
A=01001110
B=00110111
C=11111000
D=10001001
Laske A - B, A - C, A - D ja C - D
Muodostetaan ensin komplementoimalla luvut -B, -C ja -D:
B=00110111 ; -B=11001001
C=11111000 ; -C=00001000
D=10001001 ; -D=01110111
Ja varsinaiset laskut:
| A-B | A-C | A-D | C-D |
|---|
01001110
+11001001 | 01001110
+00001000 |
01001110
+01110111 | 11111000
+01110111 |
| 00010111 | 01010110 | 11000101
1
00100100 |
01101111 |
| OK | OK | Ylivuoto | OK |
Liukuvan pilkun luvuista
Liukuvan pilkun lukujen käytön perusteita:
- kiinteän pilkun esityksessä käytössä suppea lukualue. Esim. 7:llä bitillä 0-128.
(Esityspituuden lisääminen epäkannattavaa: yhden bitin lisääminen vain kaksinkertaistaa lukualueen)
- Lisäksi jos kiinteän pilkun esityksessä kasvatetaan lukualuetta, kasvattaa se myös esitystarkkuutta,
mikä on usein tarpeetonta
- liukuvan pilkun esitystavalla saadaan yleensä riittävän suuria lukuja 32 bitillä
- esityspituuden lisääminen yhdellä bitillä kasvattaa lukualuetta eksponentiaalisesti
Liukuvan pilkun luku vastaa siis desimaalijärjestelmän ilmaisua 10 eksponentteina.
(Esim. 0,5235 × 1012, 2,24 × 10-7, -1.3 ×
1030)
Liukuvan pilkun luku jakaantuu kolmeen osaan:
Eniten merkitsevä bitti on merkkibitti (sign, s).
Tämän jälkeen seuraa joukko eksponenttibittejä (exponent, e).
Lopuksi tulee mantissa. (fraction, f)
Lisäksi liukulukuun liittyy siirre (bias, b)
Esimerkki IEEE-standardin mukaisesta liukuluvusta:
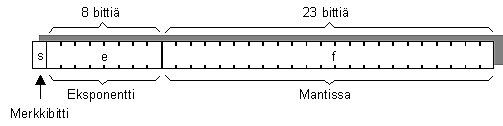
Luku = (-1)s × 2e-b × 1.f
(mantissa on siis ykköstä pienempi luku, bitit tulkitaan kakkosen negatiivisina
potensseina s.e. eniten merkitsevän kerroin on 2-1, seuraavan 2-2 jne..)
Muistettavaa:
- Eksponentti esitetään aina siirretyssä eli biasoidussa muodossa. Tässä on kyse
siitä, ettei eksponentilla ole omaa merkkibittiä, joten se on periaatteessa
aina positiivinen. Koska kuitenkin halutaan pystyä esittämään sekä negatiivisia
että positiivisiä eksponentteja, siirretään lukualuetta vasemmalle. Lukualue
siirretään siten että sen keskipiste on nollassa (tai sen vieressä, tasan siirto
ei mene). (Biasointi tulee esiin 2. laskuharjoituksessa. Ks. Myös esimerkit)
- Mantissa esitetään yleensä itseisarvomuodssa.
- Jollei ole erityistä syytä, luvut esitetään aina normaalimuodossa.
- Tarvittaessa luku skaalataan normaalimuotoon eksponenttia muuttamalla.
- Normaalimuodossa luvulla on suurin mahdollinen esitystarkkuus.
- Mantissa on normaalimuotoinen, mikäli mantissa alkaa ykkösellä.
Esimerkki 1 Tulkitse binääriluku (1001 1000 0101 0100)2 liukuvan pilkun lukuna.
Tässä tehtävässä ensimmäinen bitti on merkkibitti, eksponentti esitetään viidellä bitillä ja loput 10 kuuluvat mantissaan, joten esitys ei ole IEEE-standardin mukainen
Edetään tehtävässä seuraavasti:
- Katsotaan ensin mikä on tulevan luvun merkki (onko luku positiivinen vai negatiivinen).
Koska merkkibitti (s) on 1, luku on negatiivinen
- Tämän jälkeen tulkitaan eksponentti, eli seuraavat 5 bittiä muutetaan 10-järjestelmään, kuten on opittu aiemmin.
001102 = 610
- Koska halutaan sekä positiiviset, että negatiiviset eksponentit käytämme siirrettä (bias).
Siirteen suuruus on puolet koko lukualueen määrästä, joka eksponentilla voidaan esittää. Tässä tapauksessa eksponentti
on 5 bittiä pitkä eli sillä voidaan esittää 25 = 32 erilaista lukua. Siirteen keskipiste on nollan vieressä
(koska lukualue ei mene tasan) jolloin voidaan esittää eksponentit välillä -15 --> 16. Ts. siirre on 15
- Eksponentin (e) ollessa 610 ja siirteen (b) 1510 on e-b=-910
- Loput 10 bittiä kuuluvat mantissaan ja niiden muuntaminen 10-järjestelmään tapahtuu helposti
00010101002 = 0 × 2-1 + 0 × 2-2 + 0 × 2-3 + 1 × 2-4 +
0 × 2-5 + 1 × 2-6 + 0 × 2-7 + 1 × 2-8 = 0,0625 + 0,015625 + 0,00390625 = 0,08203125
- Lopuksi saamme siis liukuluvuksi: (-1)1 × 26-15 × 1.0820312
= 0,00211334210
Esimerkki 2 Tulkitse binääriluku (0101 1000 0111 1000)
2 liukuvan pilkun lukuna.
Ensimmäinen bitti on merkkibitti, eksponentti esitetään viidellä bitillä ja loput 10 kuuluvat mantissaan
Edetään tehtävässä seuraavasti:
- Katsotaan ensin mikä on tulevan luvun merkki (onko luku positiivinen vai negatiivinen).
Koska merkkibitti (s) on 0, luku on positiivinen
- Tämän jälkeen tulkitaan eksponentti, eli seuraavat 5 bittiä muutetaan 10-järjestelmään, kuten on opittu aiemmin.
101102 = 2210
- Koska halutaan sekä positiiviset, että negatiiviset eksponentit käytämme siirrettä (bias).
Siirteen suuruus on puolet koko lukualueen määrästä, joka eksponentilla voidaan esittää. Tässä tapauksessa eksponentti
on 5 bittiä pitkä eli sillä voidaan esittää 25 = 32 erilaista lukua. Siirteen keskipiste on nollan vieressä
(koska lukualue ei mene tasan) jolloin voidaan esittää eksponentit välillä -15 --> 16. Ts. siirre on 15
- Eksponentin (e) ollessa 2210 ja siirteen (b) 1510 on e-b=710
- Loput 10 bittiä kuuluvat mantissaan ja niiden muuntaminen 10-järjestelmään tapahtuu helposti
00011110002 = 1 × 2-4 + 1 × 2-5 + 1 × 2-6 + 1 × 2-7 = 0,0625 + 0,03125 + 0,015625 + 0,0078125 = 0,1171875
- Lopuksi saamme siis liukuluvuksi: (-1)0 × 222-15 × 1.1171875
= 14310
Lyhyesti liukuvan pilkun luvun laskutoimituksista (esitetään yleissivistyksen vuoksi)
Yhteen- ja vähennyslasku
- luvuista pienempi muutetaan normaalimuodosta muotoon, jossa lukujen eksponentit ovat samat
- mantissoilla tehdään tarvittava laskutoimitus
- eksponentiksi tulee yhteinen eksponentti
- lopuksi normalisoidaan, mikäli se on tarpeen
Kerto- ja jakolasku
- mantissoilla tehdään tarvittava laskutoimitus
- kertolaskussa eksponentit lasketaan yhteen ja summasta vähennetään siirre
- jakolaskussa jaettavan eksponentista vähennetään jakajan eksponentti ja erotukseen lisätään siirre
- lopuksi normalisoidaan, mikäli se on tarpeen
Liukuvan pilkun lukuja käsittelee ANSI/IEEE:n standardi 754-1985. Standardi on laaja ja
yksityiskohtainen ja se määritelee esitystavat ja laskutoimitukset. Standardi on laadittu
mikrotietokoneita varten. Se sisältää kaksi perusesitystapaa:
- yksinkertainen esitystarkkuus (single precision): 32 bittiä
- kaksinkertainen esitystarkkuus (double precision): 64 bittiä
Paluu päävalikkoon