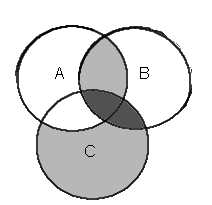
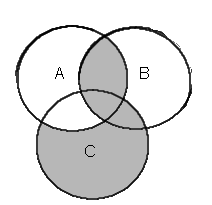
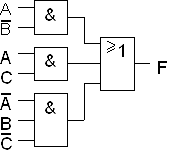
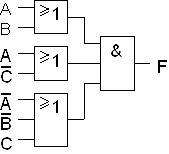
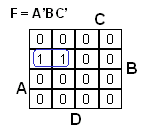
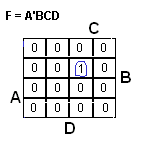
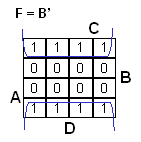
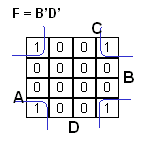
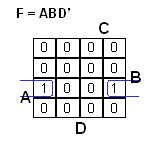
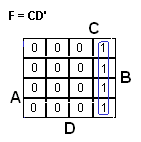
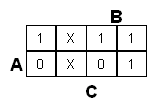Bonus 2: lausekkeen johto POS -muodosta SOP -muotoon. (Yksinkertaisempaa kuin edellinen)
- yksinkertaistetaan POS -lauseke, jos mahdollista
- kerrotaan sulut auki
- yksinkertaistetaan saatu SOP -lauseke, jos mahdollista
Karnaugh'n kartta
Eräs tehokas tapa sieventää funktioita on Karnaugh'n kartta. Se perustuu samaan ajatukseen, kuin sieventäminen
suoraan totuustaulusta, mutta on helpommin hahmotettavissa. Kartta on joukko ruutuja, jotka vastaavat täsmälleen
yhtä riviä totuustaulussa. Kunkin ruudun arvoksi tulee totuustaulun kyseisellä rivillä olevan funktion F arvo. Karnaugh'n kartan käyttöalue on 3-6 muuttujaa. 5-6 muuttujan kartat ovat jo suhteellisen
hankalia. Tätä suurempiin muuttujamääriin suosittelemme tietokoneavusteista sieventämistä.
Tutkitaan aluksi kolmen muuttujan totuustaulua:
rivi-
nro |
Input
X | Input
Y |
Input
Z | Output
F |
|---|
| 0. | 0 | 0 | 0 | 0 |
| 1. | 0 | 0 | 1 | 1 |
| 2. | 0 | 1 | 0 | 0 |
| 3. | 0 | 1 | 1 | 0 |
| 4. | 1 | 0 | 0 | 1 |
| 5. | 1 | 0 | 1 | 1 |
| 6. | 1 | 1 | 0 | 1 |
| 7. | 1 | 1 | 1 | 1 |
|
Minimitermien perusteella lausekkeeksi saataisiin F = X'Y'Z + XY'Z' + XY'Z + XYZ' + XYZ.
Oíkea muoto, mutta myös valitettavan hankala ja kaipaa paljon sievennystä. Totuustaulusta voidaan
nähdä, että jos funktio saa arvon 1 kahdella sellaisella rivillä, joiden suhteen eroa on vain
yhden muuttujan osalta, voidaan tämä muuttuja poistaa termistä. Esimerkiksi rivit 6. ja 7.: Vain
Z muuttuu eli se voidaan poistaa: XYZ'+ XYZ = XY(Z'+Z) = XY. Itseasiassa lauseke voidaan sieventää muotoon
F = X + Y'Z. Tämä olisi kuitenkin suhteellisen hankalaa taulusta lukemalla tai laskusääntöjä käyttäen.
|
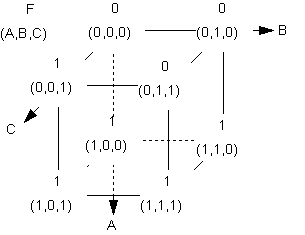
Karnaugh'n kartta on silmämääräisesti havainnollisempi. Se on kehitetty siitä ajatuksesta, että
jos yksi muuttuja vaihtelee funktion arvon sekä muiden pysyessä vakioina, voidaan kyseinen yksi
muuttuja jättää huomiotta. Tätä on helppo tarkastella sijoittamalla muuttujat moniulotteiseen
koordinaatistoon, jossa jokainen muuttuja pysyy vakiona omalla sivullaan. Särmää pitkin kuljettaessa
taas vain yksi muuttuja muuttuu kerrallaan. Esimerkiksi kuten kuvassa oikealla (Funktion arvo
kulloisessakin kuution kulmassa on merkattu kulman päälle.):
|
|
Havainnollisempi esitystapa, mutta silti suhteellisen hidas ja suuritöinen. Nopeampaan ja
yksinkertaisempaan päästään, kun vielä leikellään kuutio ja litistetään se 2-ulotteiseksi.
Tällöin täytyy vain muistaa, että reunapalat ovat edelleen vierekkäisiä. Lopputulos on
ruudukko, jota sanotaan Karnaugh'n kartaksi:
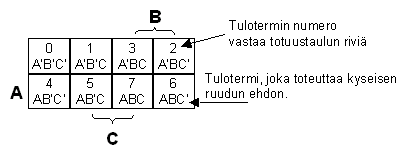
|
Karttaa tulkitaan siten, että jokainen ruutu vastaa yhtä totuustaulun riviä, eli kyseisen
rivin toteuttavaa minimitermiä. Ylläolevassa kuvassa termit on kirjoitettu näkyviin.
Huomata kannattaa, että termit 2 ja 3 sekä 6 ja 7 ovat vaihtaneet paikkaa. Tämä on
tarpeellista siksi, että sillä saadaan eri muuttujille yhtenäiset alueet, jossa ne ovat vakioita. Siis kun Karnaugh'n kartalla liikutaan ruudusta viereiseen, vain yksi muuttuja vaihtaa arvoaan.
|
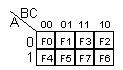
Taulussa A -muuttuja saa arvon 1 koko alarivillä. B-muuttuja taas kahdella oikeanpuoleisella
sarakkeella. C:n ykkösalue on kaksi keskimmäistä saraketta. Ruutuihin merkataan funktion arvo,
joka vastaa siis funktion arvoa samannumeroisella rivillä totuustaulussa. Viereisessä pienessä kuvassa
on vielä kartan ympärille piirretty muuttujien arvot. (A:n arvot vaihtelevat vaakariveittäin,
B:n ja C:n pystyriveittäin.)
|
|
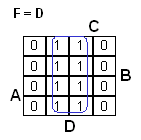
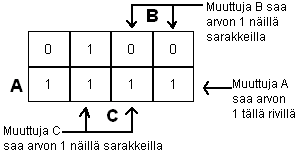
Esimerkkitaulumme kartta näyttäisi siis seuraavalta:
|
On jo huomattavasti helpompi havaita, että funktio saa arvon 1 aina, kun
muuttuja A saa arvon 1. Tämän lisäksi taulusta nähdään, että funktio saa arvon
1, kun C= 1 ja B'=1.
F = A + B'C
|
3, 4 tai 5 muuttujaa
Edellisellä sivulla esitelty kartta on tarkoitettu kolmelle muuttujalle. Neljän muuttujan kartta
on kokonaan neliö, jossa on 16 ruutua. Ruudut vastaavat neljän muuttujan totuustaulun rivejä. (Neljällä
muuttujalla saadaan aikaan 16 eri kombinaatiota.) Kannattaa muistaa, että rivi-, ruutu- tai
terminumerointi aloitetaan aina nollasta. Ohessa neljän muuttujan karnaugh'n kartta:
|
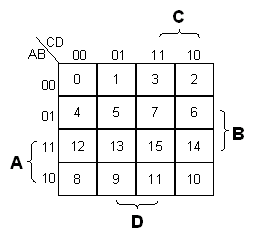
|
Kartan vasemmassa yläreunassa esitellään kartan muuttujat A, B, C, D. Nähdään, että A ja B hallitsevat
rivejä: A saa arvon yksi kahdella alimmaisella rivillä, B kahdella keskimmäisellä. C ja D hallitsevat
sarakkeita: C = 1 kahdella oikeanpuoleisista sarakkeista, D kahdella keskimmäisellä. Muuttujan nimi merkataan
niiden rivien tai sarakkeiden viereen, joilla se saa arvon 1.
Ruutujen numerointi vastaa totuustaulun rivejä (= minimitermien järjestysnumero). Nähdään, että rivien
numeroiden paikkaa on vaihdettu (2 oikeanpuoleista saraketta keskenään sekä 2 alinta riviä keskenään). Tämä tehdään,
jotta muuttujille saataisiin mahdollisimman suuret vakioalueet. (Alue, jolla muuttujan arvo pysyy vakiona.)
Kun vakioalueet ovat suuret, on helpompi silmämääräisesti erottaa kartasta alueita, joissa tietyllä muuttujalla
on vakioarvo. Kun ruudut sisältävät funktion arvon, voidaan nähdä, mistä muuttujista mikin funktion arvo
määräytyy. (Esim. jos kartan kaksi alinta riviä olisivat ykkösiä ja muut nollia, määräytyisi funktion
arvo suoraan muuttujan A mukaan. F = A)
Viisi muuttujaa
Viisi muuttujaa vaatii lisää ulottuvuuksia. Asia hoidetaan siten, että tarkastellaan kahta taulua.
Jos käytetään muuttujia A, B, C, D, E, asetetaan näistä eniten merkitsevä (A) s.e. se saa arvon 0
ensimmäisessä taulussa ja arvon 1 toisessa taulussa. Kun tutkitaan funktion käyttäytymistä, kuvitellaan
taulut päällekkäin:
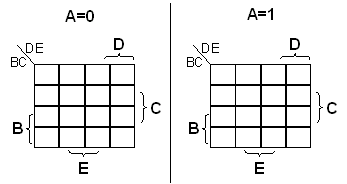
Viidellä muuttujalla saadaan 25 kombinaatiota. Tämä vastaa 32 totuustaulun riviä.
Rivit numeroidaan s.e. vasemmanpuoleinen kartta vastaa rivejä 0-15 ja oikeanpuoleinen 16-31.
Karnaugh'n kartan käyttö esimerkin avulla
Kartalla pyritään täsmälleen samaan kuin totuustaulun suhteen: muodostamaan mahdollisimman
yksinkertainen lauseke, jolla pystytään määrittelemään funktion arvo. Kartasta katsomalla siis
haetaan yksinkertaisia ehtoja muuttujille, jotta funktion arvo on haluttu kaikilla mahdollisilla
muuttujakombinaatioilla. Kartta toimii siis oikopolkuna totuustaulusta yksinkertaiseen funktion
määrittelevään lausekkeeseen.
Käytännössä tämä tapahtuu kalastamalla kartasta alueita, jotka voidaan määritellä yhdellä tai useammalla
muuttujalla tai näiden komplementeilla.
Tutkitaan kartan käyttöä neljällä muuttujalla. Otetaan
esimerkkifunktio F, joka riippuu neljästä muuttujasta A,B,C ja D ja jolle on määritelty seuraavanlainen
totuustaulu:
rivi-
nro |
Input
A | Input
B |
Input
C | Input
D | Output
F |
|---|
| 0. | 0 | 0 | 0 | 0 | 1 |
|---|
| 1. | 0 | 0 | 0 | 1 | 1 |
|---|
| 2. | 0 | 0 | 1 | 0 | 0 |
|---|
| 3. | 0 | 0 | 1 | 1 | 1 |
|---|
| 4. | 0 | 1 | 0 | 0 | 1 |
|---|
| 5. | 0 | 1 | 0 | 1 | 1 |
|---|
| 6. | 0 | 1 | 1 | 0 | 0 |
|---|
| 7. | 0 | 1 | 1 | 1 | 1 |
|---|
| 8. | 1 | 0 | 0 | 0 | 0 |
|---|
| 9. | 1 | 0 | 0 | 1 | 1 |
|---|
| 10. | 1 | 0 | 1 | 0 | 1 |
|---|
| 11. | 1 | 0 | 1 | 1 | 1 |
|---|
| 12. | 1 | 1 | 0 | 0 | 0 |
|---|
| 13. | 1 | 1 | 0 | 1 | 1 |
|---|
| 14. | 1 | 1 | 1 | 0 | 0 |
|---|
| 15. | 1 | 1 | 1 | 1 | 1 |
|---|
|
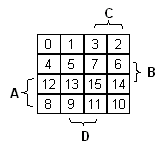
Ensimmäiseksi sijoitetaan funktion arvot Karnaugh'n karttaan. Muistin virkistämiseksi vasemalla alla esitetään
mikä totuustaulun rivi tulee mihinkin ruutuun. (Sääntö: muuten vasemmalta oikealle, ylhäältä alas; paitsi
kaksi oikeanpuoleista saraketta sekä kaksi alinta riviä vaihtavat keskenään.
! HUOM ! Edellä mainittu sääntö rivien sijoittamisesta ruutuihin pätee ainoastaan, mikäli muuttujat (nyt A,B,C ja D) määrittävät juuri ne alueet kuin esimerkeissä on näytetty. Toisinsanoen, mikäli menet vaihtamaan Karnaugh'n kartassa esim. B:n ja C:n alueiden paikkoja, ei edellämainittu sijoittelusääntö enää päde.)
Oikeanpuolimmaisessa kuvassa
funktion arvot on sijoitettu paikoilleen.
|
|
|
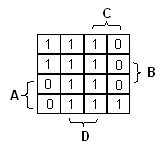
Tarkastellaan karttaa ja etsitään lauseketta funktiolle. Perussääntö on, että mitä suurempi yhtenäinen
alue voidaan saavuttaa, sen parempi, sillä sitä enemmän lauseke yksinkertaistuu. Nähdään, että funktio saa arvon 1 kahdella pystyrivillä. Näillä
muuttuja D saa myös arvon 1. Voidaan valita rivit suoraan, jolloin saadaan funktion
ensimmäinen termi: F = D + ..
|
|
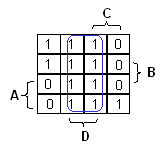
Jatketaan vaikka vasemman yläkulman ykkösillä. Kaksi ykköstä voisi valita yksinään, mutta se ei ole kannattavaa:
mitä suurempi alue saadaan valittua, sitä vähemmän muuttujia tarvitaan termiin. (Mitä vähemmän
muuttujia sitä yksinkertaisempi toteutus.) Toisaalta samoja ruutuja voi valita uudelleen. (Ei siis
haittaa, jos funktio saa arvon yksi useammalla kuin yhdellä perusteella.) Näillä perustein voidaan
ryhmitellä neljä vasemman yläreunan ruutua alueeksi ja antaa näille peruste A'C'.
|
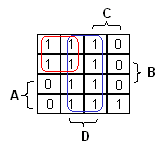
|
Jäljelle jää enää siis yksi kiusallinen ykkösruutu oikeaan alanurkkaan. Jos tähän viitataan
yksinään, vaatii se kaikkien neljän muuttujan käytön: AB'CD'. (Voi helposti todeta, että termi
on juuri tuo esim. rengastamalla alueet A, B', C, D' ja katsomalla, että ruutu jäi ulkopuolelle.)
Kannattaa yhdistää ruutu viereisen kanssa, jolloin saadaan kolmen muuttujan termi: AB'C.
|
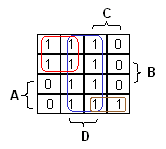
|
Näin ollen funktion lausekkeeksi saadaan F = D + A'C' + AB'C.
Karnaugh'n kartan alueiden valitseminen
Sääntöjä
- Valittu alue voi olla vain suorakaide, neliö tai jopa yksittäinen ruutu jos sitä ei saa yhdistettyä esim. reunan yli.
- Kartan reunaruudut tulkitaan vastakkaistensa kanssa vierekkäisiksi. (Alueen voi muodostaa
s.e. se menee yhden reunan yli ja jatkuu toisella.)
- Alueen koon täytyy olla joku kakkosen potenssi (1, 2, 4, 8, 16..)
- Alue ei voi saada mutkaa tai kulkea viistoon.
Muita huomattavia seikkoja:
- Mitä suurempi alue, sitä vähemmän muuttujia tarvitaan kuvaamaan sitä. -->
Pyritään siis suuriin alueisiin.
- Samoja ruutuja voi (ja usein kannattaakin) valita moneen kertaan.
- Ei kuitenkaan valita ruutuja uudelleen, jollei sillä saada kalastettua yhtään kokonaan
uutta ruutua.
- Jos ryhmä sisältää ruutuja, joista osa kuuluu vain tähän ryhmään, sanotaan
ryhmän muodostamaa termiä olennaiseksi perustermiksi.
- Jos ryhmä sisältää vain ruutuja, jotka kuuluvat muihinkin ryhmiin, sanotaan
ryhmän muodostamaa termiä perustermiksi.
- Kannattaa muodostaa vain ryhmiä, joista saadaan olennaisia perustermejä.
Esimerkkejä ryhmistä ja niiden muodostamista termeistä:
Epätäydellinen kytkentäfunktio
Toisinaan kytkentäfunktion arvolla ei ole merkitystyä tietyllä muuttujakombinaatiolla.
Tällainen tapaus on laite, jossa ei koskaan voi esiintyä tiettyä kombinaatiota tai
laite, jonka toimintaan tietyt kombinaatiot eivät vaikuta. Kohtaa vastaavaa minimitermiä
kutsutan hälläväliä-termiksi (don't care term).
Jos jonkin kombinaation arvo on jätetty määrittelemättä, sanotaan funktiota epätäydelliseksi.
Funktion arvoksi asetetaan totuustaulun kyseiseen kohtaan X. Jos kytkentäfunktio määritellään
minimitermien avulla, täytyy erikseen ilmaista X -termit.
Karnaugh'n karttaan kyseiset kohdat merkitään X:llä. Ruudut voi tulkita joko ykköseksi tai
nollaksi riippuen, kumpi tapaus on edullisempi. HUOM: Sama ruutu voi olla vain ykkönen tai nolla.
Ei siis voida rengastaa kahta aluetta puoliksi päällekkäin ja tulkita toisessa ruutu ykköseksi
ja toisessa nollaksi. (Tämä siksi, että lausekkeena määritelty kytkentäfunktio on yksikäsitteinen:
funktiolla on aina jokin arvo.)
Esimerkki kolmen muuttujan epätäydellisestä määrityksestä ja sen johtamisesta
lausekkeeksi:
Input
A | Input
B |
Input
C | Output
F |
|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | X |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | X |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
|
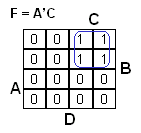
Piirretään Karnaugh'n kartta:
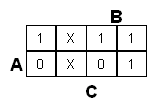
|
Ryhmitellään ja muodostetaan lauseke
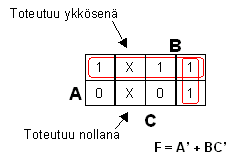
|
Karnaugh'n kartan käyttö, kun halutaan SOP -lauseke
(SOP lauseke on siis Sum Of Products eli tulojen summa.)
Säännöt, joiden mukaan edetään:
- Laaditaan totuustaulu speksien mukaan, jollei totuustaulua ole annettu jo valmiiksi.
- Piirretään totuustaulua vastaava Karnaugh’n kartta eli tarkistetaan muuttujien määrä ja tehdään sen mukaan oikean kokoinen kartta
- Siirretään totuustaulusta ykköset karttaan rivejä vastaaviin ruutuihin
- Vierekkäisistä ykkösistä muodostetaan mahdollisimman suuria ryhmiä (joiden
koot ovat kakkosen potensseja), kunnes jokainen ykköneen kuuluu johonkin ryhmään.
(Saa kuulua moneen.)
- Muodostetaan ryhmiä vastaavien tulotermien looginen summa. Se on yksinkertaisin
SOP toteutus käytetylle totuustaululle. (Mikäli ruudut on ryhmitelty oikein.)
Kannattaa muistaa, että saatu esitys ei välttämättä ole ainoa oikea.
Esimerkki tulojen summamuotoisen lausekkeen muodostamisesta neljällä muuttujalla.
Totuustaulu on annettu valmiiksi:
rivi-
nro |
Input
A | Input
B |
Input
C | Input
D | Output
F |
|---|
| 0. | 0 | 0 | 0 | 0 | 1 |
|---|
| 1. | 0 | 0 | 0 | 1 | 0 |
|---|
| 2. | 0 | 0 | 1 | 0 | 1 |
|---|
| 3. | 0 | 0 | 1 | 1 | 1 |
|---|
| 4. | 0 | 1 | 0 | 0 | 1 |
|---|
| 5. | 0 | 1 | 0 | 1 | 1 |
|---|
| 6. | 0 | 1 | 1 | 0 | 0 |
|---|
| 7. | 0 | 1 | 1 | 1 | 1 |
|---|
| 8. | 1 | 0 | 0 | 0 | 1 |
|---|
| 9. | 1 | 0 | 0 | 1 | 0 |
|---|
| 10. | 1 | 0 | 1 | 0 | 1 |
|---|
| 11. | 1 | 0 | 1 | 1 | 1 |
|---|
| 12. | 1 | 1 | 0 | 0 | 0 |
|---|
| 13. | 1 | 1 | 0 | 1 | 1 |
|---|
| 14. | 1 | 1 | 1 | 0 | 0 |
|---|
| 15. | 1 | 1 | 1 | 1 | 1 |
|---|
|
Muodostetaan 4:n muuttujan Karnaugh'n kartta ja sijoitetaan ykköset totuustaulusta rivejä vastaaviin ruutuihin (eli niitä rivejä vastaaviin ruutuihin, joilla F = 1). Muista, että kaksi oikeanpuoleisinta saraketta ovat vaihtaneet keskenään paikkaansa kuten myös kaksi alinta riviäkin (Kuten aiemmin oli opittu):
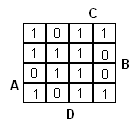
|
|
Muodostetaan alueet ja niiden perusteella funktion lauseke: esim. neljä keskimmäistä ykköstä ==> BD, kulmissa olevat ykköset ==> B'D' jne.
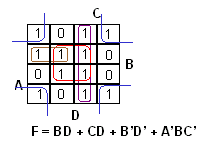
|
Karnaugh'n kartan käyttö, kun halutaan POS -lauseke
(POS lauseke on siis Product Of Sums eli summien tulo.)
POS tapauksessa kannattaa muistaa, että POS lauseke perustuu maksimitermeihin.
(Niihin funktiota kuvaaviin termeihin, jotka saavat aina arvon yksi paitsi
'omalla' totuustaulun rivillään, jolloin niiden arvo on nolla.) POS -lauseke
muodostetaan funktion komplementin eli nolla-alueiden avulla.
Säännöt, joiden mukaan edetään:
Aluksi toimitaan kuten SOP -tapauksessa eli
- Laaditaan totuustaulu speksien mukaan, jollei totuustaulua ole annettu jo valmiiksi.
- Piirretään totuustaulua vastaava Karnaugh’n kartta eli tarkistetaan muuttujien määrä ja tehdään sen mukaan oikean kokoinen kartta
- Siirretään totuustaulusta ykköset karttaan rivejä vastaaviin ruutuihin ja tarkastellaan kartan nollia.
- Muodostetaan vierekkäisistä nolla-alueista mahdollisimman suuria alueita, samaan tapaan kuin SOP-tapauksessa haettiin ykkösiä
- Muodostetaan lauseke kuten SOP-tapauksessakin. Huom ! Tämä muodostettu lauseke on nyt funktion komplementoitu lauseke siis F'
- Muodostetaan summatermien looginen tulo: Tämä saadaan muodostettua komplementoimalla F' De Morganin säänöillä. Tällöin saadaan POS-muotoinen lauseke
Kannattaa muistaa, että saatu esitys ei välttämättä ole yksikäsitteinen.
Esimerkkinä POS lausekkeen muodostaminen neljällä muuttujalla.
Käytetään samaa totuustaulua kuin POS -tapauksessa.
rivi-
nro |
Input
A | Input
B |
Input
C | Input
D | Output
F |
|---|
| 0. | 0 | 0 | 0 | 0 | 1 |
|---|
| 1. | 0 | 0 | 0 | 1 | 0 |
|---|
| 2. | 0 | 0 | 1 | 0 | 1 |
|---|
| 3. | 0 | 0 | 1 | 1 | 1 |
|---|
| 4. | 0 | 1 | 0 | 0 | 1 |
|---|
| 5. | 0 | 1 | 0 | 1 | 1 |
|---|
| 6. | 0 | 1 | 1 | 0 | 0 |
|---|
| 7. | 0 | 1 | 1 | 1 | 1 |
|---|
| 8. | 1 | 0 | 0 | 0 | 1 |
|---|
| 9. | 1 | 0 | 0 | 1 | 0 |
|---|
| 10. | 1 | 0 | 1 | 0 | 1 |
|---|
| 11. | 1 | 0 | 1 | 1 | 1 |
|---|
| 12. | 1 | 1 | 0 | 0 | 0 |
|---|
| 13. | 1 | 1 | 0 | 1 | 1 |
|---|
| 14. | 1 | 1 | 1 | 0 | 0 |
|---|
| 15. | 1 | 1 | 1 | 1 | 1 |
|---|
|
Muodostetaan Karnaugh'n kartta: (Tämä osuus on siis täysin sama kuin SOP toteutuksessa.)

|
|
Muodostetaan nolla-alueet ja niiden perusteella funktion lauseke (De Morganoimalla nollia ympyröimällä saatu F':n lauseke):
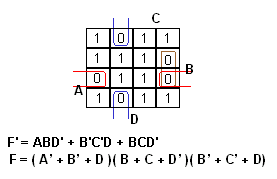
|