JA-EI (NAND)
NAND -portti saadaan laittamalla peräkkäin JA -portti (AND) ja invertteri (EI-portti, NOT):
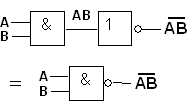
TAI-EI (NOR)
NOR -portti saadaan laittamalla peräkkäin TAI -portti (OR) ja invertteri (EI-portti, NOT):
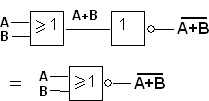
Signaalinkäsittelytekniikan laboratorio
Digitaalitekniikan perusteet - luento 5
Aikaisemmat piirikomponentit JA, TAI, EI (AND, OR, NOT) kannattaa tarvittaessa kerrata Loogiset perusfunktiot -sivulta. Tällä sivulla esitellään kaksi uutta porttia, jotka ovat hyvinkin käteviä piirisuunnittelussa. Uudet portit eivät kuulu perusporttien luokkaan siksi, että ne voidaan muodostaa yhdistelemällä perusportteja keskenään. Portteja käytetään esimerkiksi koska pelkkiä perusportteja monipuolisemmalla porttivalikoimalla on helpompi suunnitella. Myös komponenttien hinnassa on huomattavaa, että perusporteista johdetut portit voivat toisinaan olla alkuperäisiä perusportteja halvempia valmistustekniikoista riippuen.
NAND ja NOR -portit ovat siitä erityisiä, että niillä pystytään yksinään rakentamaan mikä tahansa
logiikkaporteilla toteutettavissa oleva digitaalisysteemi. (De Morganin sääntöjä
käyttäen lausekkeet voidaan aina muokata muotoon, jossa on
joko pelkkiä NAND -operaatioita tai pelkkiä NOR -operaatioita.)
|
JA-EI (NAND) 
|
TAI-EI (NOR) |
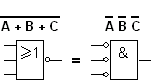 |
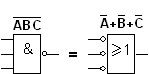 |
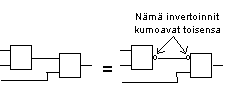
NAND- ja NOR -porteilla voidaan siis 'oikaista' kaavoja ja yksinkertaistaa funktioita. Muuta mielenkiintoista kyseisissä porteissa on, että niillä voidaan havainnollistaa myös kytkentäalgebran teoreemoja. Pari esimerkkiä alla:
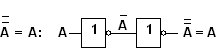 |
 |
Annettuna on SOP -muotoinen funktio F = B'C + CD + AB'D
F = B'C + CD + AB'D Kytkentäalgebran perusteella voidaan sanoa, että F'' = F. Tästä saadaan:
F'' = (B'C + CD + AB'D)''
F = (B'C + CD + AB'D)''
Edelleen voidaan sieventää De Morganin avulla, koska (A + B + C + .. + K)' = A'B'C'..K'
F=((B'C)'(CD)'(AB'D)')' Tämä lauseke voidaan toteuttaa pelkillä NAND -porteilla.
NAND -toteutus muokatulle lausekkeelle: F=((B'C)'(CD)'(AB'D)')'
Kannattaa huomata, että jos komplementit ilmaistaan viivalla, eikä pilkulla, näyttää lauseke tältä:
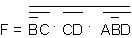
(Kyse on kuitenkin täsmälleen samasta funktiosta.)
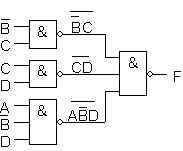
Annettuna on POS -muotoinen funktio F = C(A' + B')(A + B)
F = C(A' + B')(A + B) Kytkentäalgebran perusteella voidaan sanoa, että F'' = F. Tästä saadaan:
F'' = (C(A' + B')(A + B))''
F = (C(A' + B')(A + B))''
Edelleen voidaan sieventää De Morganin avulla, koska (A + B + C + .. + K)' = A'B'C'..K'
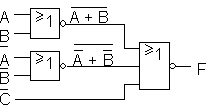
F=(C' + (A' + B')' + (A + B)')' Tämä lauseke voidaan toteuttaa pelkillä NOR -porteilla.
NOR -toteutus muokatulle lausekkeelle: F= (C' + (A' + B')' + (A + B)')'
Kannattaa huomata, että jos komplementit ilmaistaan viivalla, eikä pilkulla, näyttää lauseke tältä:
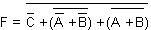
(Kyse on kuitenkin täsmälleen samasta funktiosta.)
EHDOTON TAI -portti saa arvon 1 silloin kun täsmälleen yksi sen ottosignaaleista
saa arvon yksi. Loogisen funktion lauseke on F = A'B + AB', joka merkitään
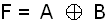 |
ja piirrosmerkki on |
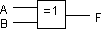 |
EHDOTON TAI -piirin selvä sukulainen on ekvivalenssipiiri 'EHDOTON-EI-TAI' (EXCLUSIVE NOR), joka saa arvon 1, jos sen molemmat ottosignaalit ovat samat. Eli F = AB + A'B'. (Piirille ei ole olemassa suomenkielistä nimeä.)
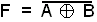 |
ja piirrosmerkki on |
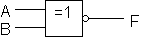 |
EHDOTON TAI -funktiolla on tiettyjä ominaisuuksia, jotka kannattaa ymmärtää: |
EHDOTON-TAI (XOR)-portin totuustaulu näyttää siis seuraavalta:
XNOR-portin totuustaulu on tietystikin XOR invertoituna. |
EHDOTON TAI -portin sovelluksia:
Siirtoportti on CMOS-tekniikalla tehty portti, joka vastaa kytkintä.
Päinvastoin kuin porteissa yleensä, siirtoportissa signaali voi kulkea
kumpaan suuntaan tahansa. Itse kytkimen lisäksi siirtoportissa on ohjaussignaali,
jonka arvo määrää, onko kytkin auki vai kiinni. Siirtoportti ei sellaisenaan
muodosta mitään tiettyä loogista funktiota, mutta sitä voidaan käyttää osana
CMOS-tekniikalla tehdyissä porteissa ja muissa piireissä.
|
Selventävä kuva:
|
Tässä siis X on varsinainen signaali ja C on ohjaussignaali. Jos C = 0, portti ei johda.
Jos taas C = 1, portti johtaa:
|
EHDOTON-TAI-funktio siirtoporteilla
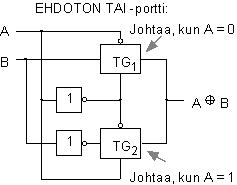
Siirtoporttien käyttö perustuu EHDOTON-TAI -funktion siihen ominaisuuteen,
että funktion arvo on toisen muuttujan (esim A) arvo sellaisenaan, jos toinen muuttuja (esim B) saa
arvon 0 ja toisen (A) arvon inversio, jos toinen (B) saa arvon 1. Allaolevassa piirissä ottosignaalin
A arvo 0 avaa siirtoportin TG1, jolloin signaali B pääsee läpi, ja arvo 1 siirtoportin
TG2, jolloin B' pääsee läpi. Saadaan siis aikaan haluttu toiminta.
Digitaalipiirit toteutetaan integroiduilla piireillä (Integrated Circuit, IC). Integroitu piiri on pieni
puolijohteesta (yleensä piistä) valmistettu hyvin pieni kappale, kutsumanimeltään siru
(engl. chip). Sirulla on n kpl toisiinsa yhdistettyjä portteja, jotka yhdessä
muodostavat integroidun piirin. Piiri pakataan muovi- tai keraamiseen koteloon, ja
se yhdistyy muuhun laitteeseen pinnien (joskus sanotaan myös jalkojen, englanniksi pins)
avulla. Pinnien määrä voi tyypillisesti vaihdella 14:stä moneen sataan kappaleeseen.
IC piirin kotelon kannessa ilmoitetaan aina piirin numero. Valmistajat taas julkaisevat
luetteloita (data book), joka sisältää kaikkien valmistajan tuottamien piirien toiminnan
kuvaukset ja muut piirisuunnittelijalle tarpeelliset asiat.
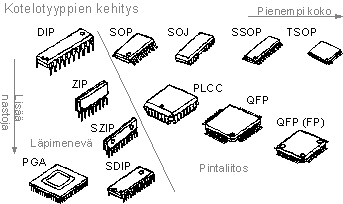
IC -piirien koko kasvaa huimasti sitä mukaa, kun kehitetään keinoja pakata samalle sirulle yhä enemmän portteja yhä pienempään tilaan. Alla on esitelty tärkeimmät kokoluokat:
Esimerkiksi tällaiselta (kuva tosin on muutaman vuoden takaa):
Integroidut piirit eroavat paitsi integrointiasteeltaan myös toteutusteknologialtaan.
Erilaisten rakennustyyppien ja piirin sisäisten perusporttien rakenteen mukaan piirit
erotellaan logiikkaperheiksi (digital logic family). Tietyn logiikkaperheen piirit ovat
keskenään yhteensopivia ja ne voidaan suoraan kytkeä toisiinsa, kun taas eri perheiden
välillä tarvitaan sovituspiirejä.
Tärkeimpiä perheitä:
Piirejä vertaillaan toisiinsa tiettyjä parametrejä käyttäen. Parametrit kuvaavat piirin erityyppisiä ominaisuuksia ja ne ovat erilaisia eri logiikkaperheillä. Alla on listattu parametreista tärkeimpiä:
Tässä kohtaa kannattaa taas muistaa, että logiikkapiireissä ykköset ja nollat ovat jännitteitä.
Piirivalmistajat määrittelevät piirien toiminnat fyysisillä tasoilla L ja H siten, että
signaalijännite UH >UL. Loogisten signaalien arvot 0 ja 1 voidaan sitoa fyysisiin tasoihin
kahdella tavalla: joko suoraan 0=L ja 1=H, jolloin puhutaan positiivisesta logiikasta tai
ristiin 0=H ja 1=L, jolloin kyseessä on negatiivinen logiikka.

|
Tämän sivun sisällöstä vastaa
aura@wooster.hut.fi URL: http://signal.hut.fi/digis/printtaa/luento5/luento5.html Sivua on viimeksi päivitetty 13.08.2003. |