Alla on kuva kombinaatiopiirin lohkokaaviosta. Lohkokaaviossa kuvataan
yksittäisillä laatikoilla piirin toiminnallisia osia. (Kombinaatiopiirissä toiminnallisia
osia on yksi kappale.)

Signaalinkäsittelytekniikan laboratorio
Digitaalitekniikan perusteet - luento 6
Kombinaatiopiirissä antosignaalien arvot riippuvat vain sen hetkisten ottosignaalien
arvoista: Piirissä on n kappaletta ottosignaaleja, jotka kulkevat digitaaliporttien läpi
(näiden digitaaliporttien muodostama kokonaisuus on siis kombinaatiopiiri). Tämän
lisäksi piirissä on m kappaletta antosignaaleja. Kombinaatiopiirit voidaan toteuttaa
esimerkiksi porttipiireillä.
(Erotuksena on kombinaatiopiireille on olemassa sekvenssipiirejä, joissa antosignaalien arvot
voivat riippua joko piirin aikaisemmista tiloista tai piirin aikaisemmista tiloista ja
nykyisistä ottosignaaleista. Sekvenssipiirejä käsitellään myöhemmin tällä kurssilla.)
Alla on kuva kombinaatiopiirin lohkokaaviosta. Lohkokaaviossa kuvataan
yksittäisillä laatikoilla piirin toiminnallisia osia. (Kombinaatiopiirissä toiminnallisia
osia on yksi kappale.)

Kun kombinaatiopiiri on toteutettu porteilla, voidaan piiri analysoida seuraavasti:
=>Piiri on analysoitu.
(Tätähän on käyty läpi aikaisemminkin.) Suunnitteluprosessi on käytännössä seuraavanlainen:
Tässä esimerkissä käydään käytännönläheinen kombinaatiopiirin suunnittelutapaus läpi.
Jotta säästettäisiin proffan koko ajatuskapasiteetti opetuskäyttöön, suunnitellaan
muistutin, joka mittaa ilman lämpötilaa ja kosteutta ja neuvoo sen mukaan
professoria joko pukemaan päällensä turkin tai ottamaan sateenvarjon mukaansa.
Muistuttimeen tulee siis sadeanturi ja pakkasanturi. Kun sadeanturi mittaa
ilmankosteuden suureksi (ottosignaali RAIN=1), syttyy sateenvarjolamppu (antosignaali UMBR=1)
palamaan. Kun taas lämpömittarin lukema laskee alle nollan celsiusasteen (ottosignaali COLD =1),
syttyy turkkilamppu (antosignaali COAT=1) palamaan.
Lisäksi laitteessa on mattoanturi, joka ilmoittaa, milloin proffa seisoo matolla (ottosignaali ONMAT =1).
(Lamppujahan ei kannata polttaa turhaan.) Lisäksi täytyy ottaa huomioon vielä tilanne
'lumisade': sateenvarjoa ei tarvita, jos on kylmä ja sataa, koska silloin sataa lunta. Tällöin muistutetaan proffaa vain takista.
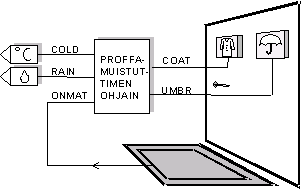
Piiri tarvitsee siis toimiakseen seuraavat signaalit:
Ottosignaalit:
Antosignaalit:
Esitetään kaikkien muuttujien (input) kaikki mahdolliset kombinaatiot:
| Input COLD |
Input RAIN | Input ONMAT |
Output COAT | Output UMBR |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
COAT = COLD × RAIN' × ONMAT + COLD × RAIN × ONMAT
= COLD × ONMAT
Tämä sievennys tulee suoraan Boolen algebran avulla: XYZ' + XYZ = XY(Z'+Z) = XY
(Eli on pakkasta ja proffa seisoo matolla. Sateesta ei välitetä.)
UMBR = COLD' × RAIN × ONMAT
(Eli ei ole pakkasta, sataa ja proffa seisoo matolla.)
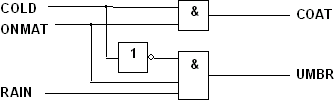
Jätetään esittämättä, koska piiri on toiminut edellisinäkin vuosina.
Aritmeettinen piiri on kombinaatiopiiri, joka suorittaa matemaattisia laskuoperaatioita.
(Esimerkiksi +, -, ×, ÷) Logiikka perustuu siihen, että loogisia tiloja '0' ja
'1' asetetaan vastaamaan binääriaritmetiikan numeroita '0' ja '1'. (Täytyy siis muistaa, että
matemaattinen 1 + 1 tarkoittaa eri asiaa kuin kytkentäalgebran 1 + 1.)
Kahden bitin summa on aina minimissään 0 ja maksimissaan 10 (=210).
Tämän vuoksi jokaisen bitin kohdalla tulokseen on varattava kaksi bittiä: varsinainen
summabitti sekä siirtobitti (tai muistibitti, engl. carry). Tämä muistibitti siirretään
seuraavaksi enemmän merkitsevän bitin laskutoimitukseen. (Ylimääräistä ongelmaa
tilan kanssa ei tule, koska 1 + 1 + 1 = 11 =(310).
Puolisummain muodostaa kahden yksibittisen luvun (X ja Y)summabitin (S) ja siirtobitin (C = carry):
|
Puolisummaimen kytkentäfunktiot ovat seuraavanlaisia:
S=X'Y + XY' = X 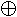 Y YC =XY Piirikaavio: 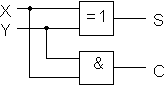
|
Kokosummain on puolisummainta kehittyneempi siinä mielessä, että se ottaa sisäänsä myös tulevan muistibitin (CI = carry in) esim. edellisestä yhteenlaskutoimituksesta. Kokosummain laskee siis kolme bittiä yhteen ja palauttaa summan (S) sekä uuden siirtobitin (CO = carry out).
|
Kokosummaimen kytkentäfunktiot:
S=X'Y'CI + X'YCI' + XY'CI' + XYCI = X  Y Y  CI CIC =X'YCI + XY'CI + XYCI' + XYCI = XY + CI(X  Y) Y)Piirikaavio: 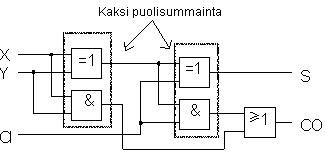 (Kun ollaan ovelia, nähdään, että kokosummain muodostuu kahdesta puolisummaimesta, joita yhdistää TAI -portti.) |
Summaimista on hyötyä vasta sitten, kun niillä voidaan käsitellä isoja lukuja. Isojen lukujen käsittelyä varten yksinkertaisesti liitetään
monia summaimia joko sarja- tai rinnakkaismuotoisesti yhteen.
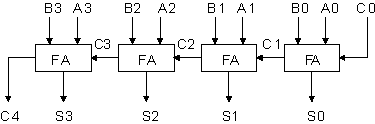
Summaimen lisäksi tärkeä operaattori on 'summain - vähennin'. Tämä on piiri, joka pystyy laskemaan sekä yhteen-
että vähennyslaskua. Tämä toteutetaan siten, että käytetään sopivaa merkkibittiä, jonka mukaan päätellään,
kumpi laskutoimitus on kyseessä: yhteenlasku suorittaa normaalin yhteenlaskuoperaation, vähennyslaskussa
täytyy muuttaa ensin vähentäjä kahden komplementtiinsa.
Binäärikertojassa yksittäisten bittien tulot lasketaan JA -piireillä. Osatulot lasketaan yhteen puolisummaimilla (Half-adder, HA).
Esimerkiksi näin:
|
Suoritetaan yksinkertainen 2 -bittisten lukujen kertolasku:
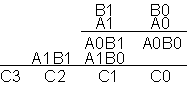
|
Piiritoteutus: 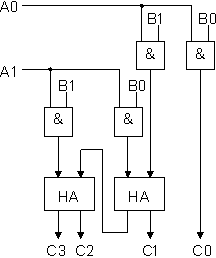
|
Dekooderi on kombinaatiopiiri, joka koodaa binäärilukuja yksikäsitteiseksi binäärikoodiksi. Käytännössä tämä tarkoittaa sitä, että dekooderi ottaa
sisään n kpl ottosignaaleja ja sillä on 2n kappaletta antosignaaleja. (Näistä ei välttämättä käytetä
kaikkia, joten asianmukaisempaa on puhua n:stä m:ään dekoodereista, missä m < 2n.)
Antosignaalit ovat ottosignaalien muodostamia minimitermejä. Siis siten, että kun ottosignaali
muodostaa kombinaation 000..00, saa vastaava antosignaali D0 arvon yksi muiden antosignaalien
saadessa arvon nolla. Edelleen kombinaatiolla 000..001, saa antosignaali D1 arvon yksi
muiden ollessa nollia jne. Eli ottosignaalien (n kappaletta) kombinaatio määrää yksikäsitteisesti mikä antosignaaleista (m kappaletta) aktivoituu. Aktivoituvia antosignaaleja on vain ja ainoastaan 1 kappale jokaista binäärilukua kohti.
|
Selvennetään asiaa esittelemällä yksinkertainen kahdesta neljään (2-4) -dekooderi. Dekooderilla on siis
kaksi ottosignaalia, joiden perusteella sillä on neljä antosignaalia. (Ottosignaalien muodostamat minimitermit.)
Kyseisen dekooderin totuustaulu näyttää seuraavalta:
|
Piirikaavio dekooderille saadaan totuustaulun perusteella:
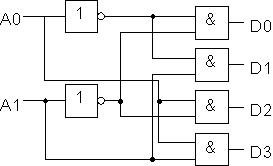
|
Usein käytetään myös invertoitua dekooderia, joka on piirikaavioltaan edellisen kaltainen, mutta siinä on
JA -porttien sijaan JAEI -portit (NAND). Tällöin totuustaulu muuttuu myös päinvastaiseksi: anto saa arvon yksi
kaikkialla muualla paitsi oman järjestysnumeronsa ilmoittavan minimitermin kohdalla, jolloin anto saa arvon
nolla. Invertoituantoisesta dekooderista on esimerkki jäljempänä.
Yleistunnus: 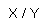
Otot merkataan binääriluvun kertoimen mukaan eli 1,2,4,8...
Annot kuvataan minimitermien numeroilla eli järjestyksessä 0 --> 2n
2-4 dekooderi: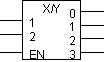
|
3-8 dekooderi: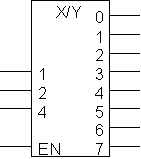
|
EN -otto on sallintaotto (enable).
Tyypillisesti arvolla EN=0, piiri ei
toimi, ja arvolla EN=1 piiri toimii
normaalisti.
Totuustaulu on muuten vastaava kuin perusdekooderilla, paitsi että annot on invertoitu ts. ottosignaalit määrittävät mikä antosignaaleista on looginen nolla, muiden ollessa ykkösiä:
| Input A0 | Input A1 | Output D3 | Output D2 |
Output D1 | Output D0 |
|
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 |
Piirissä käytetään JA -porttien sijaan JAEI -portteja:
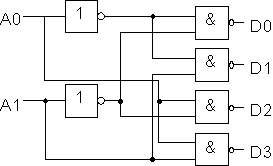
Kooderi on kombinaatiopiiri, joka muuntaa yksikäsitteistä binäärikoodia yksikäsitteiseksi binääriluvuksi
eli unaarimuodosta binaarimuotoon. Käytännössä tämä tarkoittaa sitä, että kooderin sisääntulossa on 2n kappaletta ottosignaaleja, jotka koodataan n kappaleeksi antosignaaleja.
Kooderin toiminta on siis päinvastaista aiemmin esitetyn dekooderin toimintaan nähden.
|
Selvennetään asiaa esittelemällä yksinkertainen kaksibittisen binaarikooderin (neljästä kahteen kooderin) toiminta. Kooderilla on siis
neljä ottosignaalia, joiden perusteella sillä on kaksi antosignaalia.
Kyseisen kooderin totuustaulu näyttää seuraavalta:
|
Yleistunnus: 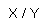
Otot kuvataan minimitermien numeroilla eli järjestyksessä 0 --> 2n
Annot merkataan binääriluvun kertoimen mukaan eli 1,2,4,8...
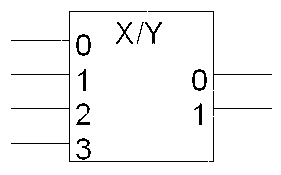
| 4-2 kooderi: |
|
EN -otto on sallintaotto (enable).
Tyypillisesti arvolla EN=0, piiri ei
toimi, ja arvolla EN=1 piiri toimii
normaalisti.
Edellä esitetyn kooderin toiminta ei ole määritelty siinä tapauksessa mikäli ottosignaaleista D3 - D0 useampi kuin yksi saa arvon 1 samanaikaisesti. Tätä varten on prioriteetti kooderi, jossa ottosignaaleiden eniten merkitsevä ykkönen määrää kooderin antokoodin. Prioriteettikooderin toiminta on kuvattu alla olevassa esimerkissä.
|
Selvennetään asiaa esittelemällä kaksibittisen prioriteettikooderin toiminta. Kooderissa siis ottosignaaleiden D3-D0
eniten merkitsevä ykkönen määrää kooderin antokoodin, jolloin kyseisen kooderin totuustaulu näyttää seuraavalta:
|
Ylläolevaan totuustaulua tarkastelemalla nähdään, että toisin kuin kooderin tapauksessa, prioriteettikooderin toiminta on määritelty riippumatta ottosignaalien ykkösten määrästä.
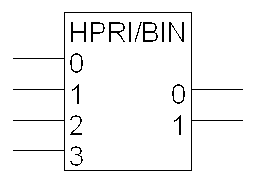
| 4-2 prioriteettikooderi: |
|
|
Tämän sivun sisällöstä vastaa
aura@wooster.hut.fi URL: http://signal.hut.fi/digis/printtaa/luento6/luento6.html Sivua on viimeksi päivitetty 13.08.2003. |