Signaalinkäsittelytekniikan laboratorio
Digitaalitekniikan perusteet - luento 8
Kiikkujen funktio on säilyttää niihin tuotu data kellojakson yli ja välittää se tämän jälkeen eteenpäin.
Kiikut ovat olennainen osa aikariippuvaisia piirejä, käytännössä tarkoitamme näilä pelkästään
synkronisia sekvenssipiirejä. (Asynkroniset sekvenssipiirit ovat erikoistapaus. Niitä ei käsitellä tällä kurssilla
sen enempää.) Synkronisen sekvenssipiirin kiikut muodostavat yhdessä rekisterin, jossa säilytetään
piirin tilaa. Salvat eivät sovellu tähän tarkoitukseen, koska niiden tila voi muuttua kesken kellojakson (kuten jo aiemmin opittiin).
Synkronisessa sekvenssipiirissä tilamuutokset tapahtuvat vain kellosignaalin tahdissa.
Kiikku muuttaa tilaansa vain kellosignaalin muuttuessa: tällöin se tarkastelee piirin nykytilaa ja sen hetkisiä ottosignaaleita ja tallettaa näiden aiheuttaman tuloksen seuraavaan kellojaksoon saakka. Sanotaan, että kellosignaali liipaisee kiikun. Tällä tarkoitetaan sitä ominaisuutta, että kiikku tarkastelee ympäristöänsä vain kellosignaalin tietyllä reunalla. Kiikut luokitellaan liipaisutavan perusteella. Kiikkutyypit:
Pulssiliipaistava kiikku ottaa dataa sisään kellopulssin nousevalla reunalla ja antaa sitä ulos kellopulssin
laskevalla reunalla.
Reunaliipaistava kiikku vaihtaa tilaansa kellopulssin aktiivisella reunalla, joka on kellosignaalin joko nouseva tai laskeva reuna. On siis olemassa
erikseen kellopulssin nousevalla ja laskevalla reunalla liipaistavia kiikkuja.
Tilanmuutos näkyy kiikun annossa joko heti tai kellosignaalin toisensuuntaisen muutoksen jälkeen. Jälkimmäisessä tapauksessa puhutaan viivästetystä
annosta.
Käytännön digitaalisuunnittelussa käytetään lähinnä pelkästään reunaliipaistavia kiikkuja. Eri kiikkutyypit on kuitenkin hyvä tuntea,
erikoistilanteiden varalta.
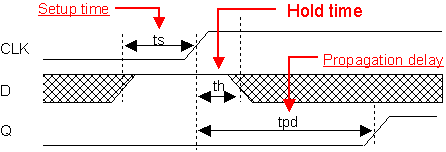
Kiikkujen yhteydessä on otettava huomioon kaksi eri varoaikaa sekä kiikusta itsestään aiheutuva viive. Varoajat ovat niitä ajanjaksoja, jolloin
kiikku ei huomaa muutoksia piirissä. Käytännössä varoajat ovat kiikulle merkityksellisen kellopulssin
reunan molemmin puolin. (Setup time eli asetusaika ennen kellopulssin nousua sekä Hold time eli pitoaika
nousun aikana sekä vähän sen jälkeen.) Tämä tarkoittaa sitä, että ottosignaalit eivät saa muuttua varoaikana
tai piirin toiminta häiriintyy.
Toinen ajoituksessa huomioitava seikka on kiikusta aiheutuva etenemisviive (propagation delay): signaalilla kestää
vähän aikaa kulkea kiikun läpi (tyypillisesti muutaman kymmenen nanosekunnin luokkaa). Allaolevassa kuvassa esitetään reunaliipaistavan D-kiikun kriittiset aikajaksot:

Huomattavaa:
Tästä eteenpäin esitellään eri kiikkutyyppejä niiden toiminnan mukaan. Tärkeimmät loogiset kiikkutyypit ovat D, JK, T ja SR.
Näistä esitellään pulssi- ja reunaliipaistavia versioita. (Kannattaa siis huomata, että jokaisesta loogisesta päätyypistä (D, JK, T, SR) voidaan
tuottaa sekä reuna-, että pulssiliipaistavia kiikkuja.)
Pulssilla määräytyminen tarkoittaa sitä, että salpa lukee piirin tilan kellopulssin nousevalla reunalla ja
antaa datan ulos kellopulssin laskevalla reunalla. Tässä esitellään esimerkkeinä pulssilla määräytyvistä salvoista
D- ja JK -salvat. HUOM! Salpojen totuustauluissa olevista merkinnöistä:
Q(t) tarkoittaa salvan tilaa ennen kellopulssia.
Merkintä Q(t+1) tarkoittaa salvan seuraavaa tilaa ts. tilaa kellopulssin jälkeen (riippuu ottosignaaleista ja salpatyypistä)
|
Pulssilla määräytyvän D-salvan piirrosmerkki ja totuustaulu.
|
Pulssilla määräytyvän D-salvan rakenne. (Voidaan muodostaa kahdesta D-salvasta, joiden rakenne oli selvitetty jo aiemmin.) 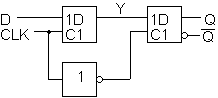
|
Pulssin aikakaavio 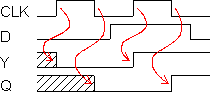
|
|
Pulssilla määräytyvän JK-salvan piirrosmerkki. Käytännössä salpa toimii kuten SR-salpa, mutta vaihtaa tilaansa aina edellisen tilan komplementtiin kun molemmat otot (J- ja K-otto) ovat ykkösiä. 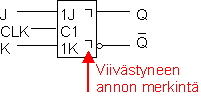
|
JK-salvan totuustaulu 
|
| Pulssin aikakaavio 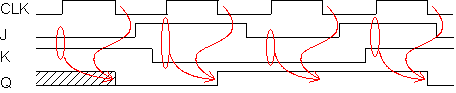
|
|
Huomaa, että J ja K-ottojen tulee pysyä stabiilina koko CLK-pulssin ajan
Kiikun tilanmuutos tapahtuu, kun kellosignaali muuttaa tilaansa (kellosignaalin aktiivinen
reuna). Vaihtoehdot ovat käytännössä, joko nousevalla tai laskevalla reunalla liipaisu tai
vastakkaisreunoin liipaisu. Kuvissa kannattaa huomata viive. Esimerkkinä esitellään D- ja JK- kiikut.
Tilanmuutos tapahtuu, kun kellosignaali muuttuu nollasta ykköseen.
|
Piirrosmerkki
|
Totuustaulu 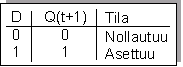
|
aikakaavio 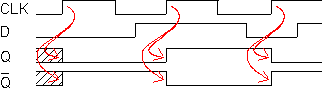
|
Tilanmuutos tapahtuu, kun kellosignaali muuttuu ykkösestä nollaan.
|
Piirrosmerkki
|
Totuustaulu 
|
aikakaavio 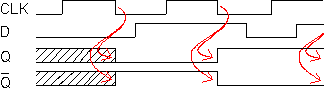
|
|
Piirrosmerkki
Totuustaulu
|
Aikakaavio 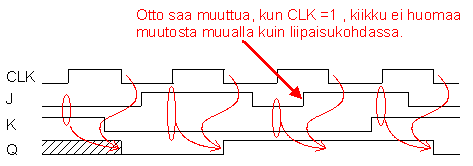
|
Tässä kerrataan vielä lyhyesti kaikki peruskiikut. Mukaan on liitetty yksi aiemmin esittelemätön kiikkutyyppi: T-kiikku. Kaikkia allaolevia kiikkuja käytetään kurssilla. Käytännön digitaalisuunnittelussa yleisin suunnittelijan näkemä kiikkutyyppi on D -kiikku. On kuitenkin huomattava, että suunnittelussa on tiettyjä perustilanteita, esimerkiksi niin sanottua 'edge detectoria' suunnitellessa, joissa on ehdottomasti käytettävä muita kiikkutyyppejä. Tämän vuoksi kaikkien kiikkutyyppien tuntemus on tärkeää. Samoin on osattava ja ymmärrettävä kiikkutyyppien toiminta.
T-kiikun toiminta on hyvin yksinkertainen. Kiikulla
on kaksi ottoa: T ja CLK (kello). Jos T-ottoon tulee nollaa, säilyttää kiikku tilansa. Jos T-ottoon
tulee ykköstä, komplementoi kiikku tilansa. Alla on esitetty nousevan reunan T-kiikun piirrosmerkki, sen totuustaulu ja aikakaavio.
Tilanmuutos tapahtuu, kun kellosignaali muuttuu nollasta ykköseen.
|
Piirrosmerkki
|
Totuustaulu 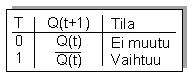
|
aikakaavio 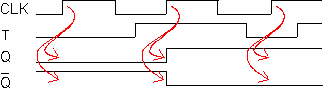
|
|
D-kiikku
T-kiikku
|
JK-kiikku
SR-salpa
|
Jos halutaan etsiä yhtäläisyyksiä ja eroavaisuuksia perheen kiikkujen välillä, voidaan huomiota kiinnittää mm. seuraaviin seikkoihin:
D-salpa
|
Pulssilla määräytyvä D-salpa
|
Nousevalla reunalla liipaistava D-kiikku
|
Nousevalla reunalla liipaistava JK-kiikku
|
Laskevalla reunalla liipaistava JK-kiikku
|
Vastakkaisreunoin liipaistava JK-kiikku
|
Vanhan kertauksena:
Digitaaliset piirit jaetaan kahteen pääluokkaan: kombinaatiopiireihin ja sekvenssipiireihin. Kombinaatiopiireissä
antosignaalien arvot riippuvat vain ottosignaalien samanhetkisistä arvoista. Sekvenssipiirit
ovat aikariippuvaisia eli arvojen annot riippuvat piirin tilasta, joka on talletettuna piiriin ja mahdollisesti myös ottosignaaleista.
Käytännössä tämä tarkoittaa sitä, että sekvenssipiiri sisältää muistavia joitain komponentteja, yleensä kiikkuja.
Sekvenssipiirit jaetaan edelleen kahteen alaluokkaan: asynkronisiin ja synkronisiin sekvenssipiireihin.
Asynkroninen piiri vaihtaa tilaansa, kun jokin sen ottosignaaleista muuttuu. Synkronisessa sekvenssipiirissä
on yksi hallitseva otto: kello-otto. Synkroninen sekvenssipiiri vaihtaa tilaansa vain tämän oton tahdissa.
Asynkronisten piirien suunnittelu ja analyysi on työlästä ja hankalaa. Tällä kurssilla käsitellään vain synkronisia
sekvenssipiirejä. Näiden analyysi ja suunnittelu on suhteellisen suoraviivaista ja opettaa digitaalilaitteiden
toiminnan perusperiaatteita.
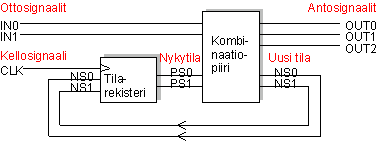
Synkroninen sekvenssipiiri koostuu kombinaatiopiiristä ja tilarekisteristä. Piirin ottosignaalit
tulevat kombinaatiopiiriosaan ja antosignaalit lähtevät siitä. Tilarekisteri on erillinen
rivi kiikkuja. Tilarekisteriin menee kombinaatiopiiristä piirin uusi tila (new state, NS) ja siitä palaa kombinaatiopiiriin
piirin nykytila (present state, PS):
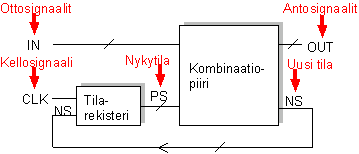
Yhteen kiikkuun voidaan tallettaa yksibittinen tieto, joko 0 tai 1. Näin ollen kullakin kiikulla on kaksi
erilaista tilaa. Tarvittava kiikkumäärä riippuu piirin tilojen määrästä: k:lla kiikulla voidaan toteuttaa
2k tilaa. Näin ollen kiikkujen ja tilojen välillä täytyy vallita seuraavanlainen suhde:
2k-1 < s =< 2k
missä s on piirin tilojen ja k tilarekisterin kiikkujen määrä.
Helpoin tapa muodostaa tilarekisteri on käyttää
D-kiikkuja. Tällöin piirin uusi tila tuodaan suoraan D-kiikun ottoihin. Joskus käytetään myös JK -kiikkuja.
Periaatteessa kiikut uudistavat tilansa jokaisen kellopulssin aktiivisella reunalla: uusi tila menee kiikkuun ja
sieltä saadaan nykytila. Käytännössä tässä täytyy kuitenkin muistaa kiikuista syntyvä viive. (Tilarekisterin annot muuttuvat vasta
viiveen jälkeen.) Piirin ulkopuolella viiveet näkyvät tilasignaaleista riippuvien antosignaalien muutoksen viivästymisenä.
Synkronisessa sekvenssipiirissä piirin antosignaalit voivat riippua pelkästään tilasta, jossa piiri on (MOORE). Toinen
vaihtoehto on, että annot riippuvat sekä piirin tilasta, että ottosignaaleista (MEALY). Synkronista sekvenssipiiriä, jonka
antosignaali ei suoraan riipu mistään ottosignaalista vaan pelkästään piirin tilasta sanotaan Mooren koneeksi. Mikäli
yksikin antosignaali riippuu jostakin ottosignaalista, on kyseessä Mealyn kone. Mealyn koneen sellaista antosignaalia,
joka riippuu suoraan yhdestä tai useammasta ottosignaalista sanotaan ehdolliseksi annoksi.
Yleensä tietyn määrittelyn mukainen piiri voidaan toteuttaa joko Mooren koneena tai Mealyn koneena. Tällöin Mooren kone
-toteutuksessa on yleensä enemmän tiloja, mutta kombinaatiopiiri saattaa olla Mealyn kone -toteutusta yksinkertaisempi.
Alla Mooren ja Mealyn koneen rakenteet:
|
Mooren kone:
|
Mealyn kone:
|
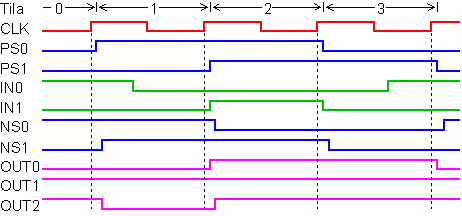
Tässä esitellään 4-tilaisen (=kaksi tilasignaalia) sekvenssipiirin lohkokaavio ja signaalien aikakaavio. Esitykset ovat suuntaa-antavia.
Näiden kahden esityksen perusteella piirin toimintaa ei voida analysoida kokonaisvaltaisesti, koska
molemmat jättävät liian paljon asioita avoimeksi. (Aikakaavio ei kuvaa signaalien kaikkia
kombinaatioita, joten piirin toimintaan jää aukkoja.)
Esimerkin on tarkoitus tuoda aika- ja lohkokaavioita tutummiksi. Aikakaaviosta pitäisi pystyä
ymmärtämään signaalien välisiä riippuvuussuhteita sekä viiveitä. Kummastakin tapauksesta on näkyvissä
ainakin yksi selkeä esimerkki.
Viive näkyy aikakaaviossa tilasignaalien osalta parhaiten. Nykytilan signaalit (PS0 ja PS1) ovat
viivästyneet hieman kun taas uuden tilan signaalit (NS0 ja NS1) ovat viivästyneet hieman enemmän.
Mikäli viivettä ei olisi lainkaan tapahtuisi muutos näissä signaaleissa täsmälleen samaan aikaan
kellopulssin (CLK) muutoksen kanssa. Nyt ei kuitenkaan ole näin.
Signaalien välinen riippuvuussuhde näkyy kun tarkastellaan aikakaaviota seuraavasti: Nousevalla
kellonreunalla (CLK) piirin "tarkastaa" ottosignaalit (IN0 ja IN1), sekä piirin nykytilan (PS0 ja PS1). Näiden perusteella piiri muodostaa uuden tilan (NS0 ja NS1) sekä antosignaalit (OUT0, OUT1 ja OUT2)
(Lisäksi voidaan havaita, että OUT0 on täsmälleen sama signaali kuin PS0. Se on vain viivästynyt hieman)
Mealyn kone on kaikkein yleisin synkroninen sekvenssipiiri. Jopa toinen pääluokka, Mooren kone,
voidaan esittää Mealyn koneen erikoistapauksissa. Tällä sivulla käsitellään (kytkentämalleiltaan)
erityyppisiä sekvenssipiirejä. Näistä ehdottomasti tärkein ryhmä on erilaiset laskurit (counter). Muut voi lukaista
yleissivistyksen vuoksi.
Peruslaskuri
|
Ohjattava laskuri
|
Sekvenssipiirin rajatapaus |
Synkronoiva rekisteri: |
Asynkronisia ottoja |
|
Sekvenssipiirin toteutus jakaantuu vaiheisiin. Työn kuluessa voidaan joutua palaamaan uudelleen aikaisempiin vaiheisiin.
Aluksi määritellään piirin toiminta. Määrittely on yleensä sanallinen kuvaus piirin toiminnasta.
Piiriä tarkastellaan ulkoa päin, eikä sen otto- ja antosignaaleja vielä määritellä tarkasti. Sanallinen
määrittely voi olla yksinkertaisille piireille pari lausetta, mutkikkaille hyvinkin laaja. Määrittelyyn
voidaan liittää vuokaavio, jos se auttaa asiaa.
Määrittelyn pohjalta laaditaan piirin lohkokaavio. Lohkokaavio kuvaa piirin toiminnalliset osat, ei
varsinaista toimintaa. Monimutkainen piiri jaetaan mielekkäisiin lohkoihin, koska monen pienen lohkon
suunnitteleminen on helpompaa kuin yhden suuren. Lohkokaavioon merkitään näkyviin lohkojen väliset signaalit sekä
piirin ulkoiset signaalit.
Määritellään lohko ja piirretään siitä tilakaavio joko tavallisena tilakone-esityksenä tai ASM -kaaviona (opetetaan myöhemmin).
Tämän jälkeen toteutetaan lohkot käytettävissä olevilla piireillä ja piirretään piirikaaviot. (Nykyään on
käytössä myös laitteiston korkean tason kuvauskieliä. Tällainen on esimerkiksi VHDL -kieli. Mikäli lohko
kuvataan VHDL:ää käyttäen, ei välttämättä tarvita ollenkaan tilakone- tai ASM -mallia, vaan tietokone
laatii tarvittavan mallin kuvauksen perusteella.)
Simuloidaan piiri käytettävissä olevilla simulaattoriohjelmilla. Ohjelma matkii piirin toimintaa ja tutkii
sen toimintaa erilaisilla ottosignaalisekvensseillä. Näin pyritään selvittämään, toimiiko piiri määrittelyn
edellyttämällä tavalla. Virheiden löytyessä palataan takaisinpäin toteutusvaiheissa ja korjataan virheet.
Tämän jälkeen rakennetaan prototyyppi ja tutkitaan sen toimintaa mittalaitteilla. Sekä palataan taas taaksepäin
korjaamaan lisää ilmenneitä virheitä. Nykyisin pyritään havaitsemaan virheet simulointivaiheessa, koska se on
huomattavasti halvempaa ja nopeampaa. Simulointi- ja rakennusvaiheissa virheitä löytyy usein moneen kertaan, joten
korjaus ja uudelleen testaus -vaiheita täytyy uusia.
Sekvenssipiirejä mallinnetaan siis tilakoneita piirtämällä. Näissä piirroksissa pyritään graafisesti esittämään, miten
piirin toiminnan historia vaikuttaa piirin toimintaan tällä hetkellä tai tulevaisuudessa. Kansanomaisemmin ilmaistuna
tilakaaviossa tarkastellaan kysymystä:
Jos piiri aiemmin oli tietyssä tilanteessa (piirin nykytila) ja sai tietyn syötteen (ottosignaalit), niin minkälaiseen tilanteeseen piiri joutuu seuraavaksi (uusi tila)
ja minne se tulee menemään, jollain tietyllä syötteellä?
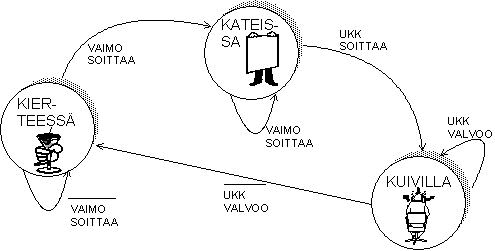
Esimerkkinä tästä mallinnuksesta on alla poliitikon tilakone. Tässä tilanteessa tutkittavaa piiriä vastaa poliitikko. Poliitikko voi olla kolmenlaisessa eri tilanteessa (kierteessä, kateissa tai kuivilla). Piirin syötteitä (ottosignaalit) vastaavat vaimo ja UKK. Riippuen syötteistä poliitikko voi joko pysyä tilanteessa, jossa hän valmiiksi on tai siirtyä seuraavaan.
|
Tämän sivun sisällöstä vastaa
aura@wooster.hut.fi URL: http://signal.hut.fi/digis/printtaa/luento8/luento8.html Sivua on viimeksi päivitetty 8.10.2008. |