Signaalinkäsittelytekniikan laboratorio
Digitaalitekniikan perusteet - luento 9
Tilakaavio (state diagram) ja sen käyttö
Synkronisella piirillä on joukko eri tiloja. Nämä tilat muodostavat takaisinkytkentöjä ja sijoittuvat piiri-/lohkokaaviossa seuraavasti:
'uusi tila' on se tilasignaalien joukko, joka menee tilarekisterin kiikkuihin sisään. 'Nykytila'
on se tilasignaalien joukko, joka saadaan kiikuista ulos. Synkroniset sekvenssipiirithän koostuivat
tilarekisteristä (= joukko kiikkuja) sekä kombinaatiopiiriosasta. Synkroninen sekvenssipiiri on siis tilakone.
Tila kuvaa aikariippuvuutta ja sillä on erilaisia ominaisuuksia joita ovat mm. tilakoodi sekä tilaan liittyvät annot. Tilakoodi
vastaa suoraan niitä nollia ja ykkösiä, joita saadaan kiikuista piiriin, kun ollaan kyseisessä tilassa.
(Esim. 4 kiikkua, tilakoodi 0110. Kyseisessä tilassa kiikkujen annot ovat 0, 1, 1, ja 0.) Jos tilaan liittyy anto, joka
on riippuvainen vain tilasta (ei lainkaan ottosignaaleista, esim. Mooren koneessa on vain tilaan liittyviä antoja), kirjoitetaan
anto kauttaviivan toiselle puolelle muodossa: tilakoodi / tilaan suoraan liittyvä anto. (Ks. myös graafinen esimerkki alempaa)
Tilasta voidaan liikkua toiseen tilaan tai pysyä samassa tilassa. Tilasta toiseen liiikkuminen tapahtuu tiettyjen tilaehtojen
avulla. Käytännössä uusi tila saavutetaan aina seuraavan kellojakson alussa. (Synkronisen sekvenssipiirin ominaisuuksiinhan
kuuluu, että piiri vaihtaa tilaansa vain kellopulssin tahdissa.) Tilasiirtymä kuvataan tilakaaviossa nuolella. Nuolen
yläpuolelle kirjoitetaan sen ottosignaalin kyseinen arvo, joka mahdollistaa siirtymän tilasta toiseen. Jos lähtötilaan liittyy ottosignaalista riippuvia
antoja, ilmoitetaan annot kauttaviivan toisella puolella muodossa: ottosignaali / signaalista riippuva anto.
... ja sama graafisin esimerkein
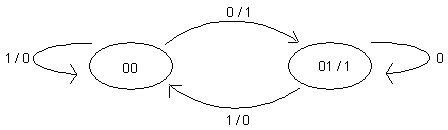
Tilakaaviossa jokaista piirin tilaa kuvaa soikio. Soikion sisällä on kyseisen tilan tilakoodi (Esim. tässä tapauksessa piiri on tilassa 00) |
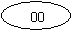
|
Jos tilaan liittyy anto, joka riippuu vain tilasta, ilmaistaan se tilan yhteydessä kauttaviivan toisella puolella seuraavasti: (esim. tässä tapauksessa kun piiri on tilassa 00, on piirin antosignaali 1) |
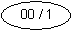
|
Tilasiirtymät tilasta toiseen tilaan esitetään nuolilla. Nuolen yläpuolelle merkitään sen ottosignaalin kyseinen arvo, joka mahdollistaa tilasiirtymän (esim. tässä tapauksessa ottosignaalin tulee olla 0): |
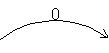
|
Jos lähtötilassa on ottosignaalista riippuva anto, merkataan kyseinen anto
ottosignaalin seuraksi tilasiirtymään kauttaviivan toiselle puolelle (esim. tässä tapauksessa mikäli ottosignaali saa arvon 0 ja suoritetaan tilasiirtymä, antaa piiri antosignaalin arvoksi 1:n) |
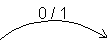
|
Yksinkertainen tilakaavio voisi näyttää vaikka tältä: (Esimerkki olisi
tosielämässä hyvin kömpelö. Siihen on lähinnä pyritty mahdutettamaan
kaikki pääasiat tilakaaviosta.) |
|
|
Tätä ylläolevaa tilakaaviota voidaan tulkita seuraavalla tavalla:
- Kun piiri on tilassa 00 (tilakoodi=00) ei näytä tapahtuvan mitään.
- Kun tilassa 00, ottosignaali on 1. Tällöin piirin "ulosanti" eli antosignaali saa arvon 0.
- Kun tilassa 00, ottosignaali onkin 0, antaa piiri antosignaalina 1:en ja siirtyy samalla tilaan 01
- Tilassa 01 antosignaali on koko ajan 1
- Kun tilassa 01 ottosignaali on 0, piiri vain pysyy samassa tilassa kuin ennenkin (siis tilassa 01)
- Kun taas tilassa 01 ottosignaali onkin 1, vaihtaa piiri tilaansa takaisin tilaan 00 ja samalla antosignaalin arvoksi tulee 0.
ASM (Algorithmic State Machine)
ASM -kaavio on perinteisen tilakaavion graafisesti havainnollisempi muoto. ASM -kaavio ei ole
yhtä yleismaailmallinen kuin perinteinen tilakaavio, mutta se on toisaalta huomattavasti
selkeämpi ja siten takaisinpäin synkronisten sekvenssipiirien suunnittelussa.
ASM kaavio piirretään ASM:n toiminnallisen määrittelyn ja lohkokaavion perusteella. Se kuvaa
yksikäsitteisesti synkronisen sekvenssipiirin toiminnan ja sisältää kaiken piirin toteuttamisen
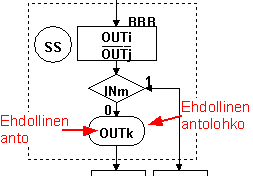
kannalta tarpeellisen informaation. ASM -kaaviossa on symboleja (tila, anto, päätöslohko sekä ehdollinen anto)
ja niihin liittyviä merkintöjä. Symbolit kuvaavat siis ASM:n tiloja, tilasiirtymiä ja niihin liittyviä
ehtoja. Merkinnät antavat lisätietoja.
ASM -kaavion pääkohdat
Myöhemmissä esimerkeissä (luennot 9 ja 10) esitellään ASM-kaavion käyttöä osana synkronisen
sekvenssipiirin suunnittelua. Tässä käydään kuitenkin lyhyesti yhteenvetona läpi tärkeimät
ASM -kaavion merkinnät:
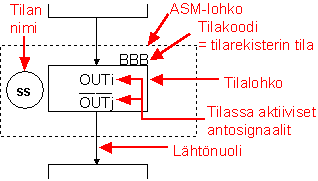
- tila = suorakaide, tilakoodi ilmoitetaan suorakaiteen oikeassa yläkulmassa
- tilan nimi on ilmoitettu ympyrän sisällä, tilaa kuvaavan suorakaiteen vieressä
- päätöslohko = ehto tilasiirtymälle (ottosignaalin nimi) = salmiakki, jossa on ehtona päätökseen vaikuttavan ottosignaalin
nimi. Vaihtoehtojen (ottosignaalin arvo 1 tai 0) mukaan lähtee nuolet salmiakin kulmista
uusiin (päätöstä seuraaviin) tiloihin
- tilaan liittyvä antosignaali = antosignaalin nimi, joka on kirjoitettu tilalohkoon sisälle. Tämä antosignaali toteutuu aina ko. tilassa
- anto, joka riippuu suoraan ottosignaalista = ehdollinen anto = pyöristetty suorakaide. Tämä seuraa päätöslohkon jälkeen, jolloin ottosignaali on siis vaikuttanut antosignaaliin (= ehdollisuus). Tätä käytetään Mealyn-koneissa. Antosignaali saa ko. arvon ainoastaan mikäli ottosignaali toteutuu (vrt. normaali antosignaali)
- tilasiirtymä = jos tilasta A voi siirtyä tilaan B, on niiden välillä nuoli. Nuoli voi
kulkea erilaisten päätöslohkojen kautta.
ASM (Algorithmic State Machine) -kaavion osat
Tila ja siihen liittyvät symbolit: |
|
|
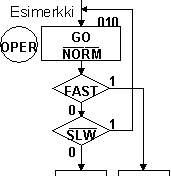
Esimerkin tulkinta:
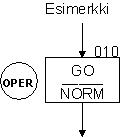
- Kyseisen tilan tilakoodi (tilan oik. yläkulmassa) on 010 (Tätä tarvitaan myöhemmin, kun kytketään kiikkuja yhteen)
- Tilan nimi on OPER
- Tilan annot ovat: GO sekä (NORM)'
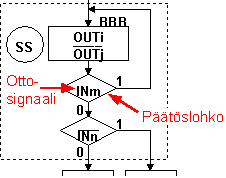
Päätöslohko - huomattavaa: ottosignaalin vaikutus kuvataan päätöslohkolla. Jokaista tilanmuutokseen
vaikuttavaa ottosignaalia varten on oma päätöslohko. Lohkot ovat peräkkäin, eivät rinnakkain. |
|
|
- Tilan tilakoodi on 010
- Tilan nimi on OPER
- Tilan annot ovat: GO sekä (NORM)'
- Ottosignaaleina ovat FAST sekä (SLW)'. Näistä ottosignaalilla FAST on korkeampi prioriteetti, joten se "tarkastetaan" ensiksi.
- Mikäli otto FAST = 1, etenee laite uuteen tilaan (uuden tilan tilakoodia ei kuvassa näy). Tässä tapauksessa on merkityksetöntä, mikä on ottosignaali (SLW)':n arvo.
- Mikäli otto FAST = 0, siirrytään tarkastelemaan ottoa (SLW)'.
- Mikäli (SLW)'= 0, edetään uuteen tilaan (jonka tilakoodia ei kuvassa näy). (Edellyttäen, että FAST=0)
- Mikäli (SLW)'= 1, edetään takaisin vanhaan tilaan (eli pysytään koko ajan samassa tilassa OPER, jonka tilakoodi on 010)
Ehdollinen anto: anto, joka riippuu suoraan jostain ottosignaalista |
|
|
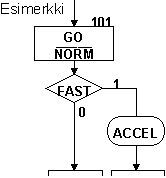
- Tilan tilakoodi on 101
- Tilan annot ovat: GO sekä (NORM)'
- Ainoana ottosignaalina on FAST.
- Mikäli otto FAST = 0, etenee laite uuteen tilaan (uuden tilan tilakoodia ei kuvassa näy).
- Mikäli otto FAST = 1, etenee laite uuteen tilaan (uuden tilan tilakoodia ei kuvassa näy). Samalla laite antaa myös antosignaalin ACCEL (eli ACCEL=1, muutenhan sitä ei merkitä ASM-kaavioon lainkaan)
- Huom! Antosignaali ACCEL on siis ehdollinen anto, jonka laite antaa vain jos otto FAST=1
ASM -esim 1: yksinkertainen tilaketju
Toiminnan määrittely
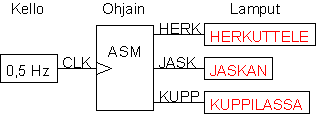
Suunnitellaan valomainos, jossa teksti vilkkuu oheisen kaavion mukaan. Valopaneeli
on ensiksi tyhjä, sitten paneeliin ilmestyy yksi kerrallaan sanat HERKUTTELE, JASKAN ja KUPPILASSA. Tämän jälkeen näyttö tyhjenee jälleen.
Jokainen erilainen valonäyttö on yksi tila. Sanat ovat laitteen antosignaaleja. Kellojakso on 2 sekuntia:
|

|
Lohkokaavio
Lohkokaavio määrittelee piirin toiminnalliset osat. Laatiminen ei ole välttämätöntä, mutta voi selkeyttää
suunnittelua isompien piirien ollessa kyseessä. Tässä esimerkissä rakennetaan neljätilainen sekvenssipiiri.
Tilat toistuvat peräkkäin aina samanlaisina ja samassa järjestyksessä (piiri on siis teoreettisesti laskuri, joka laskee 0 --> 3), joten ottosignaaleja
ei kellon lisäksi ole:
|
|
ASM -kaavio
Jokaiselle tilalle täytyy määritellä tilalohko, nimi ja tilakoodi.
Tilakoodit voidaan valita halutusti, kunhan se on jokaiselle tilalle yksilöllinen. Yleensä pyritään
nimeämään tilat jossakin loogisessa järjestyksessä. (Esim. 4 tilaa: 00, 01, 10, 11). Tilakoodin koko pyritään
pidetään mahdollisimman pienenä, koska mitä suurempi tilakoodi on, sitä enemmän tarvitaan kiikkuja. Käytännössä bittien määrä juontuu 2-kantajärjestelmän mukaisesti. Mikäli
piirissä on s tilaa, tarvitaan bittejä k = log2s kokonaisluvuksi pyöristettynä. Ylimääräisiä
bittikombinaatioita kutsutaan käyttämättömiksi tiloiksi. Tilakoodien valinta vaikuttaa siis piirin monimutkaisuuteen.
Suoraan ei kuitenkaan voida päätellä, mikä koodivalinta olisi optimaalisin.
Tilat voidaan nimetä mielivaltaisella tavalla. Järkevää on kuitenkin nimetä ne nimillä, jotka jotenkin kuvaavat ko. tilaa. Esimerkissämme tilat on nimetty:
EI (näytöllä ei ole mitään, tilakoodi=00), H (näytöllä lukee HERKUTTELE, tilakoodi=01), HJ (näytöllä lukee HERKUTTELE JASKAN, tilakoodi=10), sekä HJK (näytöllä lukee HERKUTTELE JASKAN KUPPILASSA, tilakoodi=11)
|
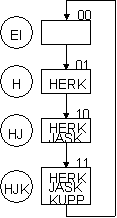
|
Jos kaivataan täsmällisempää lohkokaaviota, voidaan se tehdä esim. ASM-kaavion perusteella:
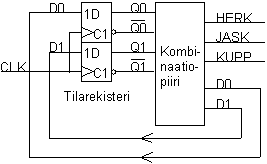
D-kiikkujen määrä (2 kpl) saadaan suoraan tilakoodin suuruudesta (4 tilaa = 2 numeroa). Se, että kiikut ovat juuri D-kiikkuja on vedetty hatusta ja kiikkujen tyyppi otetaan huomioon kunnolla vasta kombinaatiopiiriä suunnitellessa.
Tässä kuvassa Q0 ja Q1 (sekä niiden komplementit) ovat nykytilan signaaleja ja D0 sekä D1 ovat uuden tilan signaaleja. Kombinaatiopiiri on esitetty vasta lohkokaaviotasolla.
Seuraavalla sivulla käydään läpi kombinaatiopiirin muodostaminen.
Kombinaatiopiirin toteutuksen suunnittelu

|
ASM -kaaviosta saadaan tilataulukko:
nykytila = tila, joka tulee kiikuista
uusi tila = tila, joka
menee kiikkuihin
|

|
Tilataulu (joka siis muistuttaa totuustaulua) muodostetaan seuravasti:
- Aloitetaan ASM-kaavion ensimmäisestä tilasta nimeltä "EI" (tila 00), joka merkitään nykytilaksi.
- Merkitään samalle riville uudeksi tilaksi se tilakoodi, johon ASM:n nuoli osoittaa vanhasta tilasta siis tila "H" (eli tilakoodi = 01).
- "Annot"-kohtaan kirjoitetaan mitkä ovat piirin antosignaalit tilassa 00, ja niitähän ei ole (valomainos on siis tyhjä), joten kaikki annot on merkattu nollaksi.
Käydään vielä tilataulun toinen rivi läpi...
- Merkataan nykytilaksi tila 01 (siis tila "H"). Tästä tilasta lähtee nuoli seuraavaan tilaan, jonka tilakoodi on 10.
- Uusi tila on siis 10 eli tila "HJ"
- Annot tilassa 01 ovat:HERK=1, JASK=0 ja KUPP=0. Tämä tarkoittaa sitä, että kyseisessä tilassa valotaululla palaa ainoastaan sana "Herkuttele"
Samalla tavalla käydään läpi kaikki tilat ja lopuksi saadaan muodostettua tilataulu, joka yllä oli esitetty
Tilataulukon perusteella saadaan lausekkeet tilakiikkujen D-otoille.
Koska tilasiirtymään vaikuttaa vain edellinen tila, tutkitaan vain taulun osia
nykytila ja uusi tila.
Tässä kohtaa tulee vaikuttamaan se, että on valittu D-kiikku toteutus. Toteutus on nyt helppo ja menee seuraavalla tavalla:
Tehdään taulukko, joka kertoo meille D-kiikkujen ottosignaalit.
Nyt tuijotetaan ensin tilataulukon sarakkeita Q1 ja D1. Tämä kertoo meille miten kiikku nro1 muuttaa tilaansa. Siis
kysymys kuuluu: Mikä on D-kiikun oton (eli D:n) arvo kun tila muuttuu
| Q1 | --> | D1 |
0 | --> | 0 |
0 | --> | 1 |
1 | --> | 1 |
1 | --> | 0 |
(eli tässä on sarakkeet Q1 ja D1 kopioitu tilataulusta)
Muistellaan D-kiikun muutostaulua (ks. edellinen luento "kiikkuyhteenveto"), ja sehän oli seuraavanlainen.
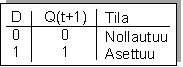
| Ja tästä saadaan siis D-kiikku nro1:en D-oton arvoiksi: | Ja tästä saadaan siis D-kiikku nro0:n D-oton arvoiksi: |
| Q1 | --> | D1 | ==> | D1-otto |
0 | --> | 0 | ==> | 0 |
0 | --> | 1 | ==> | 1 |
1 | --> | 1 | ==> | 1 |
1 | --> | 0 | ==> | 0 |
|
| Q0 | --> | D0 | ==> | D0-otto |
0 | --> | 1 | ==> | 1 |
1 | --> | 0 | ==> | 0 |
0 | --> | 1 | ==> | 1 |
1 | --> | 0 | ==> | 0 |
|
Tästä saadaan sitten Karnaugh'n avulla varsinaiset lausekkeet kiikkujen otoille (sijoitellaan 1:set jo opittuun tapaan kartalle) :
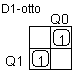 : D1 = Q0Q1' + Q0'Q1 : D1 = Q0Q1' + Q0'Q1
|
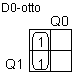 : D0 = Q0' : D0 = Q0'
|
Seuraavaksi määritellään lausekkeet annoille (sijoitellaan 1:set Karnaugh'n kartalle):
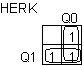 : HERK = Q0 + Q1 : HERK = Q0 + Q1
|
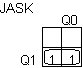 : JASK = Q1 : JASK = Q1
|
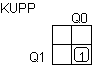 : KUPP = Q0Q1 : KUPP = Q0Q1
|
Tämän jälkeen toteutetaan lausekkeet porttipiireillä (ja muistetaan, että kiikuista lähtee ulos nykytila):
|
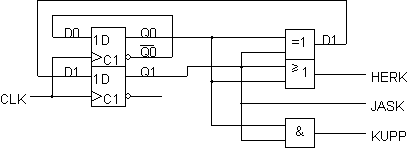
|
ASM esim 2: Piiri, jossa on tilanmuutoksiin vaikuttavia ottosignaaleja
Toiminnan määrittely
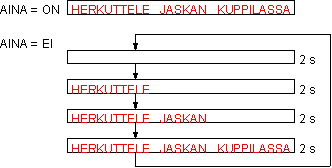
Monimutkaistetaan edellistä mainosta hieman. Lisätään siihen kytkin, joka pitää piirin joko vakiotilassa,
jolloin koko teksti on näkyvissä tai sitten aiheuttaa normaalin tilakierron. Piiri toimii siis oheisen
kaavion mukaan:
|
|
Lohkokaavio
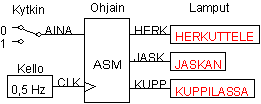
Määrittelyn mukaan piirin toimintaan vaikuttaa yksi ottosignaali: "AINA". Tämän vaikutus täytyy näkyä lohkokaaviossa.
Muuten lohkokaavio pysyy edellisen esimerkin mukaisena.
|
|
ASM -kaavio
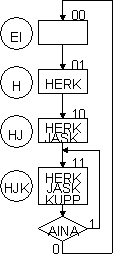
Ottosignaalin vaikutus näkyy ASM -kaaviossa päätöslohkona (salmiakki): jos AINA = 1, palataan aina takaisin HJK -tilaan, jossa
kaikki sanat siis palavat yhtäaikaa. Jos AINA = 0, kierretään tavallista tilaketjua. ASM kaavio voitaisiin myös piirtää
siten, että ottosignaali AINA tarkistettaisiin jokaisessa tilassa. (Nythän, jos AINA muuttuu ykköseksi jossain tiloista EI,
H, HJ, huomataan muutos vasta tilassa HJK.) Jos tilanmuutosta tarkkailtaisiin useammin, toimisi laite tarkemmin speksien
mukaan. Valomainoksen tapauksessa asia ei kuitenkaan ole oleellinen.
|
|
ASM esim 2, piirin toteutuksen suunnittelu

|
ASM -kaaviosta saadaan tilataulukko:
nykytila = tila, joka tulee kiikuista
uusi tila = tila, joka
menee kiikkuihin
X-merkintä tilataulukossa tarkoittaa sitä, että kyseisellä ottosignaalilla ei ole vaikutusta ts. aivan sama onko se 0 vai 1.
Koska X-merkintä vastaa 0 tai 1:stä niin rivi 00X onkin kaksi riviä (000 ja 001) Jos kaikki rivit kirjoittaisi tällä tavalla "auki" saataisiin normaalin kokoinen tilataulukko (siis 8 rivinen 3:lla muuttujalla, koska 23=8)
|

|
Tilataulukon perusteella saadaan lausekkeet tilakiikkujen D-otoille.
Kiikkuja on edelleen kaksi, mutta niihin vaikuttaa yhteensä kolme signaalia: molemmat nykytilat sekä otto AINA.
Tässäkin tapauksessa molempien kiikkujen D-otot vastaavat suoraan D1 ja D0 sarakkeita
Karnaugh'n avulla saadaan lausekkeet kiikkujen otoille:
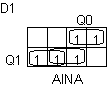 : D1 = Q0Q1' + Q0'Q1 + Q1AINA : D1 = Q0Q1' + Q0'Q1 + Q1AINA
|
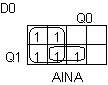 : D0 = Q0' + Q1AINA : D0 = Q0' + Q1AINA
|
Seuraavaksi märitellään lausekkeet annoille. Kannattaa huomata, että annot ovat riippuvaisia vain tiloista,
ei ottosignaalista:
 : HERK = Q0 + Q1 : HERK = Q0 + Q1
|
 : JASK = Q1 : JASK = Q1
|
 : KUPP = Q0Q1 : KUPP = Q0Q1
|
Tämän jälkeen toteutetaan lausekkeet porttipiireillä:
|
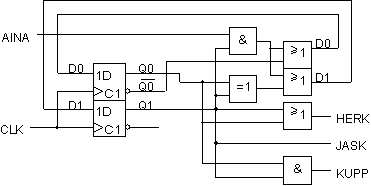
|
Paluu päävalikkoon














 : D1 = Q0Q1' + Q0'Q1
: D1 = Q0Q1' + Q0'Q1
 : D0 = Q0'
: D0 = Q0'
 : HERK = Q0 + Q1
: HERK = Q0 + Q1
 : JASK = Q1
: JASK = Q1
 : KUPP = Q0Q1
: KUPP = Q0Q1





 : D1 = Q0Q1' + Q0'Q1 + Q1AINA
: D1 = Q0Q1' + Q0'Q1 + Q1AINA
 : D0 = Q0' + Q1AINA
: D0 = Q0' + Q1AINA
