SIGNAL PROCESSING IN TELECOMMUNICATIONS RESEARCH GROUP

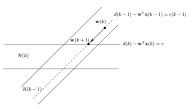
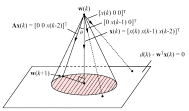
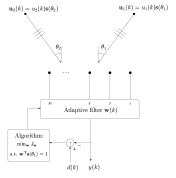
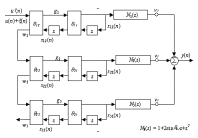
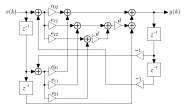
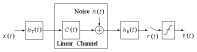
This research investigates new data selective adaptive filtering algorithms. The algorithms are derived under the concept of set-membership filtering (SMF) and also use the concept of data reusing. The algorithms include a data-dependent step-size that provides fast convergence. The results show considerable performance improvement using the new algorithms for correlated input signals compared with the recently proposed set-membership NLMS (SM-NLMS) algorithm. The BNDR-LMS algorithm which uses consecutive data pairs in each update, has shown fast convergence for correlated input signals. However, the fast convergence comes at the expense of a higher misadjustment, because the algorithm utilizes the data even if it does not imply innovation. In order to combat the conflicting requirements of fast convergence and low misadjustment, the objective function of the adaptive algorithm needs to be changed. Set-membership filtering (SMF) specifies a bound on the magnitude of the estimation error. The SMF can be seen as a generalization of the set-membership identification (SMI) technique to include a more general filtering problem. The SM-NLMS algorithm only uses the current input-desired signals in its update. To overcome this problem we investigate several versions of an algorithm that uses data from successive time instants in order to construct a set of feasible solutions for the update.

This research analyzes partial-update normalized adaptive filters. Partial-update adaptive filtering is a technique suitable for applications where the order of the adaptive filter is so high that it may impair even the implementation of low computational complexity algorithms, such as the NLMS algorithm. Partial-update adaptive filters reduce the algorithm complexity by properly decreasing the number of filter coefficients that is updated each iteration so that the filter order may be kept fixed. Order statistics are used to analyze the mean-squared error of the adaptive filter output.

Adaptation algorithms that satisfy linear constraints find applications in various areas of communications, e.g., in antenna array processing and multiuser detection. In this project, new linearly constrained adaptive filtering (LCAF) algorithms are derived and analyzed, which are tailored to specific applications and have advantageous performance regarding convergence and robustness. The computational complexity encountered in LCAF algorithms is not only due to the adaptation algorithm employed. The LCAF perform updates in a subspace orthogonal to the space spanned by their set of linear constraints. Therefore, the LCAF algorithms usually contain a projection matrix, and the form of this matrix affects the computational complexity of the implementation. In certain cases, the projection matrix can contribute to the final computational complexity, as much a high-computational complexity algorithm would do. To address this problem, a method is proposed where a transformation is applied to the input signal to reduce the dimension of the problem such that the adaptation can be performed in a reduced subspace.

This research investigates IIR realization of adaptive notch filters. The focus is on the filter structure and updating algorithms in dealing with multiple notches. Algorithms used include gradient descent algorithms, Steiglitz_McBride, or hyperstable algorithms, to name a few. Furthermore, our investigation focuses on lattice structure realizations utilizing their structrual orthoganolity. We are trying to find out efficeint algorithms that keep the convergence points in alignment, at the notch frequencies. This research includes also analysis of the convergence properties, analysis of the relationship of the frequency estimation errors, analysis of the signal to noise ratios, and characterisation of the stationary points.

This research investigates efficient algorithms and implementation structures for the purpose of timing synchronization in communication systems. The more efficient algorithms and implementation structures aim to lower the complexity and cost of the communication devices while improving their performance.

This project investigates efficient joint transmit and receive filter algorithms and implementation structure for wireline and wireless channels. The algorithms are derived by simultaneous Nyquist and matched filter criteria with transmit power constraints. The main idea is to reduce the complexity of the decision-feedback (DFE) equalizer at the receiver.

In this project, techniques for adaptive algorithms to estimate and equalize channels with nonlinearities are considered. The main goal is to alleviate the linearity requirements of transmit amplifiers by allowing distortion which is compensated for in the receiver. Both memoryless nonlinearities and those with memory are considered.