The complex Kautz filter

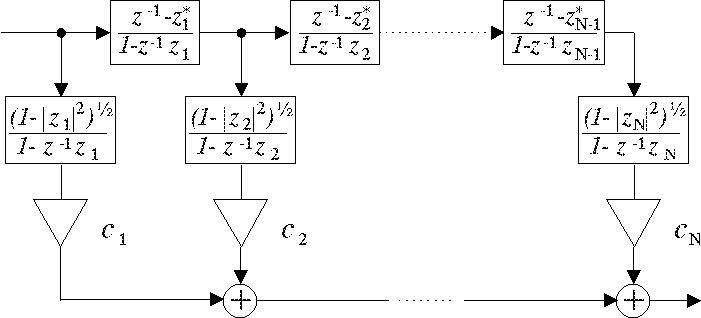
Figure: the general (complex) Kautz filter consists of an all-pass backbone, and all-pole tap-output filters, with corresponding normalization terms. The tap-output filter and the subsequent all-pass block are coupled, as can be seen. FIR and Laguerre filters are special cases of the Kautz filter, with all poles at z=0 or z=a, -1<a<1, respectively.

The complex Kautz filter is completely determined by a set of poles and the filter weights:

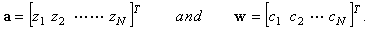
The Matlab function S=compkautz(a,M,x) produces (length M) responses to input vector x. The response of the filter is then the matrix product y=S*w. The filter order is (defined to be) N=length(a).