The real Kautz filter 

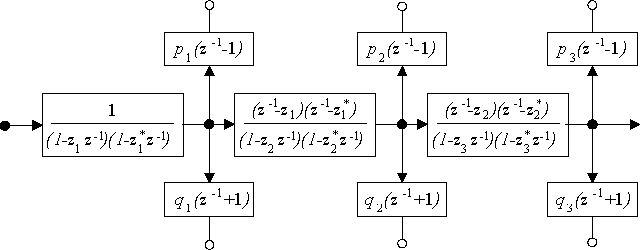
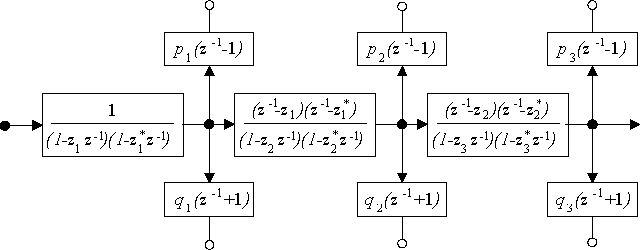
Figure: the real Kautz filter (depicted here for purely complex poles) consists of cascaded second-order blocks and dual tap-outputs. Shifting the denominators one step to the right and compensating the change in the tap-output filters restores the transversal all-pass structure. 

Tap-outputs of the real Kautz filter are completely determined by a set of complex conjugate pole pairs:

The normalization coefficient are defined by the poles and they are given by

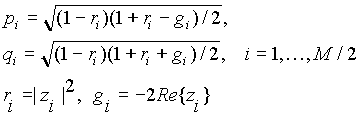
The (length N) tap-output responses to input x are produced by S=mixkautz1(a,N,x). The response of the filter with filter coefficient vector w is the product y=S*w. Notice that we can integrate the filter and normalization coefficients. If there are real poles in a, mixkautz1.m will treat them with a corresponding first-order block. Actually poles with imag(a)<0 are disregarded to avoid duplication produces by conjugate pair poles and to reduce typing.