Sivukartta
Sanasto
Laskuharjoitukset
Kytkentäalgebran teoreemoja eli Boolean Algebra
Loogiset funktiot toimivat osittain suoraan binääriaritmetiikan mukaan. Erojakin löytyy, yleisin lienee TAI -funktiossa oleva 1 + 1 = 1. Kytkentäalgebrassa JA -funktiota sanotaan loogiseksi tuloksi ja TAI -funktiota loogiseksi summaksi. Kytkentäalgebran (eli ns. Boolean algebran) tärkeimpiä teoreemoja on listattu alle:
| Yhden muuttujan teoreemoja: | |||
|---|---|---|---|
| X + 0 = X | X × 1 = X | ||
| X + 1 = 1 | X × 0 = 0 | ||
| X + X = X | X × X = X | ||
| X + X' = 1 | X × X' = 0 | ||
| Monen muuttujan teoreemoja: | |||
| X + Y = Y + X | XY = YX | kommutatiivisuus | |
| X + (Y + Z) = (X + Y) +Z | X(YZ) = (XY)Z | assosiatiivisuus | |
| X( Y + Z) = XY + XZ | X + YZ = (X + Y)(X + Z) | distributiivisuus | |
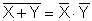 | 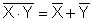 | De Morgan | |
Nämä siis ovat suoraan laskusääntöjä, joita saa (ja pitää) käyttää digitaalisuunnittelussa. Näiden sääntöjen mukaan
toimivat myös digitaalisuunnittelussa käytettävät portit, jotka esitellään myöhemmin. Monen muuttujan teoreemien
viimeisellä rivillä esitetään
ns. De Morganin kaavat. Ne käsittelevät siis komplementtia sellaisessa tapauksessa, jossa
komplementoidaan kerralla enemmän kuin yksi muuttuja (yleensä lauseke tai osa siitä).
De Morganin teoreema on tärkeä suunnittelussa, koska sen avulla voidaan saada erilaisia
toteutuksia samalle loogiselle lausekkeelle. De Morganin teoreema voidaan yleistää n >=2
muuttujalle. (Jätetään lukijan pohdittavaksi, miten.)
Teoreemoista puhutaan paljon lisää myöhemmin, kun käsitellään kytkentäfunktioita. (Kytkentäfunktio
on siis lauseke, joka sisältää edellä esitettyjä funktioita ja joka voidaan toteuttaa lopulta
esim. porttipiireillä.)
Luento 3
-
Merkkikoodit
-
Virheentarkistuksesta
-
Kytkentäalgebra ja
logiikkapiiri
-
Loogiset
perusfunktiot
- Kytkentäalgebran
teoreemoja
-
Porttipiirit
-
Funktion kolme
esitystapaa
Lisätietoja: