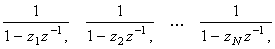
Kautz filters – Matlab scripts and demos

Tuomas Paatero

Helsinki University of Technology

Laboratory of Acoustics and Audio Signal Processing

http://www.acoustics.hut.fi/

December 7, 2000

 

Introduction 

Kautz filters [3], or generalized transversal filters, are fixed-pole filters organized structurally to produce orthonormal tap-output impulse responses. They can be seen as an orthonormal counterpart of a particular generalized linear-in-parameter structure [4] [5]: functions

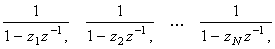
with distinct and stable poles, span an approximation space for any causal and stable (CS) signal or CS linear time-invariant system, i.e., there is an unique (least-square) optimal weighted linear combination, "parametrization", of these functions. An orthonormalization process applied to this set of functions produce functions of the form

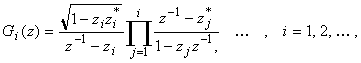
A weighted sum of these functions clearly reduces to a transversal Kautz filter, completely determined by the pole set and the weights. In general, the poles don’t have to be distinct.

The Kautz filter tap-output signals are complex valued for complex poles. However, from a sequence of real or complex conjugate pair poles it is always possible to form real orthonormal structures. This can again be seen as an operation applied to the tap-output signals, i.e., a unitary rotation operator. The real Kautz filter is a transversal structure of second-order blocks and dual tap-outputs, corresponding to the complex poles, and first-order sections for the real poles. From the infinite variety of possible solutions we have utilized one particular, which is maybe the simplest real Kautz filter structure composed from complex pole pairs [2].  

The toolbox

The included Matlab functions and a demo data file are available as a zip-file. Download and unzip the files somewhere, e.g. creating a directory \toolbox\kautz, and set the Matlab path.

There are four types of functions:

To get more information about the scripts use Matlab help or inspect directly the m-files. There is also a description of the functions for those who are still doubtful.

Some remarks

This document is a bare statement of the existence of something called "Kautz filters", almost without any connection to the theoretical and historical background, and with very few references. This is justified in many ways. To begin with, this is a software site and we are hoping to bring about a more comprehensive site elsewhere. In second place, there is actually no need or obligation to drag around the whole armament: basic concepts (e.g. orthogonality, stability, convergence results, computational complexity and numerical robustness) are well at hand.

Please contact me for further information or to report bugs and lapses on this site. mailto:tuomas.paatero@hut.fi

Acknowledgements

The Academy of Finland project "Sound source modeling" has supported this work. I would also like to thank Henri Penttinen for being the "guinea pig", and for valuable suggestions.

References

  1. H.Brandenstein and R. Unbehauen, "Least-Square Approximation of FIR by IIR Filters", IEEE Transactions on Signal Processing, vol. 46, no. 1, pp. 21 - 30, 1998.
  2. P. W. Broome, "Discrete Orthonormal Sequences", Journal of the Association for Computing Machinery, vol. 12, no. 2, pp. 151 - 168,1965.
  3. W. H. Kautz, "Transient Synthesis in the Time Domain", IRE Transactions on Circuit Theory, vol. CT-1, pp. 29 - 39,1954.
  4. T. Paatero, "Generalized Linear-in-parameter Models", in Proc. 1999 Finnish Signal Processing Symposium (FINSIG’99), pp. 217 - 221, Oulu, Finland, May 31,1999. (Finsig.pdf)
  5. T. Paatero, "Parametrien suhteen lineaarinen mallirakenne ja signaalinkäsittely", Licentiate’s Thesis 2000, http://www.acoustics.hut.fi/publications/theses.html#lic.

HUT Acoustics Logo

 

This URL: http://www.acoustics.hut.fi/software/kautz/kautz.htm
Last modified: 17.1.2001
Author: <tuomas.paatero@hut.fi>