Sivukartta
Sanasto
Laskuharjoitukset
Liukuvan pilkun luvuista
Liukuvan pilkun lukujen käytön perusteita:
- kiinteän pilkun esityksessä käytössä suppea lukualue. Esim. 7:llä bitillä 0-128.
(Esityspituuden lisääminen epäkannattavaa: yhden bitin lisääminen vain kaksinkertaistaa lukualueen) - Lisäksi jos kiinteän pilkun esityksessä kasvatetaan lukualuetta, kasvattaa se myös esitystarkkuutta, mikä on usein tarpeetonta
- liukuvan pilkun esitystavalla saadaan yleensä riittävän suuria lukuja 32 bitillä
- esityspituuden lisääminen yhdellä bitillä kasvattaa lukualuetta eksponentiaalisesti
Liukuvan pilkun luku vastaa siis desimaalijärjestelmän ilmaisua 10 eksponentteina.
(Esim. 0,5235 × 1012, 2,24 × 10-7, -1.3 ×
1030)
Liukuvan pilkun luku jakaantuu kolmeen osaan:
Eniten merkitsevä bitti on merkkibitti (sign, s).
Tämän jälkeen seuraa joukko eksponenttibittejä (exponent, e).
Lopuksi tulee mantissa. (fraction, f)
Lisäksi liukulukuun liittyy siirre (bias, b)
Esimerkki IEEE-standardin mukaisesta liukuluvusta:
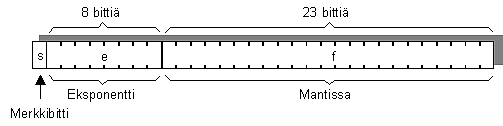
Luku = (-1)s × 2e-b × 1.f
(mantissa on siis ykköstä pienempi luku, bitit tulkitaan kakkosen negatiivisina
potensseina s.e. eniten merkitsevän kerroin on 2-1, seuraavan 2-2 jne..)
Muistettavaa:
- Eksponentti esitetään aina siirretyssä eli biasoidussa muodossa. Tässä on kyse siitä, ettei eksponentilla ole omaa merkkibittiä, joten se on periaatteessa aina positiivinen. Koska kuitenkin halutaan pystyä esittämään sekä negatiivisia että positiivisia eksponentteja (pieniä ja suuria lukuja varten), siirretään lukualuetta vasemmalle. Lukualue siirretään siten että sen keskipiste on nollassa (tai sen vieressä, tasan siirto ei mene). (Biasointi tulee esiin 2. laskuharjoituksessa. Ks. myös esimerkit)
- Mantissa esitetään yleensä itseisarvomuodssa.
- Jollei ole erityistä syytä, luvut esitetään aina normaalimuodossa.
- Tarvittaessa luku skaalataan normaalimuotoon eksponenttia muuttamalla.
- Normaalimuodossa luvulla on suurin mahdollinen esitystarkkuus.
- Mantissa on normaalimuotoinen, mikäli mantissa alkaa ykkösellä.
Esimerkki 1 Tulkitse binääriluku (1001 1000 0101 0100)2 liukuvan pilkun lukuna.
Tässä tehtävässä ensimmäinen bitti on merkkibitti, eksponentti esitetään viidellä bitillä ja loput 10 kuuluvat mantissaan, joten esitys ei ole IEEE-standardin mukainen
Edetään tehtävässä seuraavasti:
- Katsotaan ensin mikä on tulevan luvun merkki (onko luku positiivinen vai negatiivinen).
Koska merkkibitti (s) on 1, luku on negatiivinen - Tämän jälkeen tulkitaan eksponentti, eli seuraavat 5 bittiä muutetaan 10-järjestelmään, kuten on opittu aiemmin.
001102 = 610
- Koska halutaan sekä positiiviset, että negatiiviset eksponentit käytämme siirrettä (bias).
Siirteen suuruus on puolet koko lukualueen määrästä, joka eksponentilla voidaan esittää. Tässä tapauksessa eksponentti on 5 bittiä pitkä eli sillä voidaan esittää 25 = 32 erilaista lukua. Siirteen keskipiste on nollan vieressä (koska lukualue ei mene tasan) jolloin voidaan esittää eksponentit välillä -15 --> 16. Ts. siirre on 15 - Eksponentin (e) ollessa 610 ja siirteen (b) 1510 on e-b=-910
- Loput 10 bittiä kuuluvat mantissaan ja niiden muuntaminen 10-järjestelmään tapahtuu helposti
00010101002 = 0 × 2-1 + 0 × 2-2 + 0 × 2-3 + 1 × 2-4 + 0 × 2-5 + 1 × 2-6 + 0 × 2-7 + 1 × 2-8 = 0,0625 + 0,015625 + 0,00390625 = 0,08203125
- Lopuksi saamme siis liukuluvuksi: (-1)1 × 26-15 × 1.0820312
= 0,00211334210
Ensimmäinen bitti on merkkibitti, eksponentti esitetään viidellä bitillä ja loput 10 kuuluvat mantissaan
Edetään tehtävässä seuraavasti:
- Katsotaan ensin mikä on tulevan luvun merkki (onko luku positiivinen vai negatiivinen).
Koska merkkibitti (s) on 0, luku on positiivinen - Tämän jälkeen tulkitaan eksponentti, eli seuraavat 5 bittiä muutetaan 10-järjestelmään, kuten on opittu aiemmin.
101102 = 2210
- Koska halutaan sekä positiiviset, että negatiiviset eksponentit käytämme siirrettä (bias).
Siirteen suuruus on puolet koko lukualueen määrästä, joka eksponentilla voidaan esittää. Tässä tapauksessa eksponentti on 5 bittiä pitkä eli sillä voidaan esittää 25 = 32 erilaista lukua. Siirteen keskipiste on nollan vieressä (koska lukualue ei mene tasan) jolloin voidaan esittää eksponentit välillä -15 --> 16. Ts. siirre on 15 - Eksponentin (e) ollessa 2210 ja siirteen (b) 1510 on e-b=710
- Loput 10 bittiä kuuluvat mantissaan ja niiden muuntaminen 10-järjestelmään tapahtuu helposti
00011110002 = 1 × 2-4 + 1 × 2-5 + 1 × 2-6 + 1 × 2-7 = 0,0625 + 0,03125 + 0,015625 + 0,0078125 = 0,1171875
- Lopuksi saamme siis liukuluvuksi: (-1)0 × 222-15 × 1.1171875
= 14310
Lyhyesti liukuvan pilkun luvun laskutoimituksista (esitetään yleissivistyksen vuoksi)
Yhteen- ja vähennyslasku
- luvuista pienempi muutetaan normaalimuodosta muotoon, jossa lukujen eksponentit ovat samat
- mantissoilla tehdään tarvittava laskutoimitus
- eksponentiksi tulee yhteinen eksponentti
- lopuksi normalisoidaan, mikäli se on tarpeen
Kerto- ja jakolasku
- mantissoilla tehdään tarvittava laskutoimitus
- kertolaskussa eksponentit lasketaan yhteen ja summasta vähennetään siirre
- jakolaskussa jaettavan eksponentista vähennetään jakajan eksponentti ja erotukseen lisätään siirre
- lopuksi normalisoidaan, mikäli se on tarpeen
Liukuvan pilkun lukuja käsittelee ANSI/IEEE:n standardi 754-1985. Standardi on laaja ja yksityiskohtainen ja se määritelee esitystavat ja laskutoimitukset. Standardi on laadittu mikrotietokoneita varten. Se sisältää kaksi perusesitystapaa:
- yksinkertainen esitystarkkuus (single precision): 32 bittiä
- kaksinkertainen esitystarkkuus (double precision): 64 bittiä
Luento 2
Lisätietoja: