Nykyinen kymmenjärjestelmämme on perua hedelmällisen puolikuun alueelta ja se on syntynyt jonkin verran ennen ajanlaskumme alkua. Kymmenjärjestelmä perustuu nimensä mukaisesti luvun kymmenen eri potensseihin. Käytetyt numeroarvot ovat 0,1,2,3,4,5,6,7, 8, 9.

Kymmenjärjestelmä voidaan tulkita muodossa:


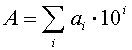
, missä a_i on jokin kerroin välitä [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Esimerkiksi luku 3025 tarkoittaa oikeastaan lauseketta 3 × 10³ + 0 × 10² + 2 × 10¹ + 5 × 10⁰.

Toisena esimerkkinä luku 1978, joka tarkoittaa samaa kuin lauseke 1 × 10³ + 9 × 10² + 7 × 10¹ + 8 × 10⁰.

Eli ensin tuhannet, sitten sadat, kymmenet ja lopuksi ykköset.

Edellä kuvatun ymmärtäminen on tärkeää, jotta voidaan laskea yhteyksiä lukujärjestelmistä toisiin. 10 (eli desimaali) -järjestelmä ei ole läheskään ainoa mahdollinen. Muita paljon käytettyjä ovat erityisesti digitaalilogiikassa käytetty 2-kantajärjestelmä (binääri), 8-kantajärjestelmä (oktaali) ja 16-kantajärjestelmä (heksadesimaali).

Alla olevasta taulukosta nähdään eri lukujärjestelmien vastaavuuksia:

Heksadesimaali	Desimaali	Oktaali	Binääri
0	0	0	0
1	1	1	1
2	2	2	10
3	3	3	11
4	4	4	100
5	5	5	101
6	6	6	110
7	7	7	111
8	8	10	1000
9	9	11	1001
A	10	12	1010
B	11	13	1011
C	12	14	1100
D	13	15	1101
E	14	16	1110
F	15	17	1111

Taulukosta nähdään, että numeroita minimoidakseen kannattaa käyttää mahdollisimman suurikantaista järjestelmää: siinä missä heksadesimaalijärjestelmässä selvitään yhdellä numerolla joudutaan binäärijärjestelmässä pahimmillaan käyttämään neljää numeroa ilmaisemaan samaa lukua. Binäärijärjestelmän laskutoimitukset ovat kuitenkin niin yksinkertaisia, että se on monissa tilanteissa kannattavin vaihtoehto.

Ihmiselle luontevin näyttää olevan desimaalijärjestelmä. Laitteissa taas tarkoituksesta riippuen yleensä kannattaa käyttää jotain muuta järjestelmää. (Lähes aina binäärijärjestelmää tai sen monikertaa eli oktaali- tai heksadesimaalijärjestelmää.) Silloin tulostus- ja syöttölaitteita varten tarvitaan muunnoksia lukujärjestelmästä toiseen.

Hyvän digitaalisuunnittelijan tulisi osata perusteellisesti binääri-, oktaali- ja heksadesimaalijärjestelmien väliset suhteet. Samoin tulisi osata nopeasti ratkaista, mitä tietty kymmenjärjestelmän luku on näissä kolmessa järjestelmässä. Lukujärjestelmämuunnoksia esitellään tarkemmin seuraavilla sivuilla.

edellinen sivu       seuraava sivu