Sivukartta
Sanasto
Laskuharjoitukset
Karnaugh'n kartta
Eräs tehokas tapa sieventää funktioita on Karnaugh'n kartta. Se perustuu samaan ajatukseen, kuin sieventäminen
suoraan totuustaulusta, mutta on helpommin hahmotettavissa. Kartta on joukko ruutuja, jotka vastaavat täsmälleen
yhtä riviä totuustaulussa. Kunkin ruudun arvoksi tulee totuustaulun kyseisellä rivillä olevan funktion F arvo. Karnaugh'n kartan käyttöalue on 3-6 muuttujaa. 5-6 muuttujan kartat ovat jo suhteellisen
hankalia. Tätä suurempiin muuttujamääriin suosittelemme tietokoneavusteista sieventämistä.
Tutkitaan aluksi kolmen muuttujan totuustaulua:
|
Minimitermien perusteella lausekkeeksi saataisiin F = X'Y'Z + XY'Z' + XY'Z + XYZ' + XYZ.
Oíkea muoto, mutta myös valitettavan hankala ja kaipaa paljon sievennystä. Totuustaulusta voidaan
nähdä, että jos funktio saa arvon 1 kahdella sellaisella rivillä, joiden suhteen eroa on vain
yhden muuttujan osalta, voidaan tämä muuttuja poistaa termistä. Esimerkiksi rivit 6. ja 7.: Vain
Z muuttuu eli se voidaan poistaa: XYZ'+ XYZ = XY(Z'+Z) = XY. Itseasiassa lauseke voidaan sieventää muotoon
F = X + Y'Z. Tämä olisi kuitenkin suhteellisen hankalaa taulusta lukemalla tai laskusääntöjä käyttäen.
|
|
Karnaugh'n kartta on silmämääräisesti havainnollisempi. Se on kehitetty siitä ajatuksesta, että
jos yksi muuttuja vaihtelee funktion arvon sekä muiden pysyessä vakioina, voidaan kyseinen yksi
muuttuja jättää huomiotta. Tätä on helppo tarkastella sijoittamalla muuttujat moniulotteiseen
koordinaatistoon, jossa jokainen muuttuja pysyy vakiona omalla sivullaan. Särmää pitkin kuljettaessa
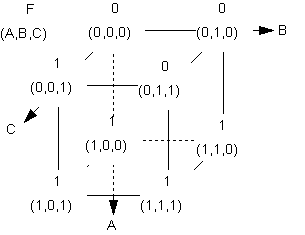
taas vain yksi muuttuja muuttuu kerrallaan. Esimerkiksi kuten kuvassa oikealla (Funktion arvo
kulloisessakin kuution kulmassa on merkattu kulman päälle.):
|
|
Havainnollisempi esitystapa, mutta silti suhteellisen hidas ja suuritöinen. Nopeampaan ja
yksinkertaisempaan päästään, kun vielä leikellään kuutio ja litistetään se 2-ulotteiseksi.
Tällöin täytyy vain muistaa, että reunapalat ovat edelleen vierekkäisiä. Lopputulos on
ruudukko, jota sanotaan Karnaugh'n kartaksi:
|
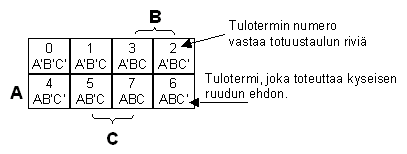
Karttaa tulkitaan siten, että jokainen ruutu vastaa yhtä totuustaulun riviä, eli kyseisen
rivin toteuttavaa minimitermiä. Ylläolevassa kuvassa termit on kirjoitettu näkyviin.
Huomata kannattaa, että termit 2 ja 3 sekä 6 ja 7 ovat vaihtaneet paikkaa. Tämä on
tarpeellista siksi, että sillä saadaan eri muuttujille yhtenäiset alueet, jossa ne ovat vakioita. Siis kun Karnaugh'n kartalla liikutaan ruudusta viereiseen, vain yksi muuttuja vaihtaa arvoaan.
|
|
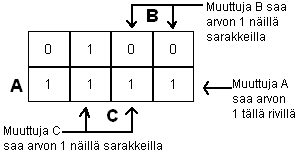
Taulussa A -muuttuja saa arvon 1 koko alarivillä. B-muuttuja taas kahdella oikeanpuoleisella
sarakkeella. C:n ykkösalue on kaksi keskimmäistä saraketta. Ruutuihin merkataan funktion arvo,
joka vastaa siis funktion arvoa samannumeroisella rivillä totuustaulussa. Viereisessä pienessä kuvassa
on vielä kartan ympärille piirretty muuttujien arvot. (A:n arvot vaihtelevat vaakariveittäin,
B:n ja C:n pystyriveittäin.)
|
|
|
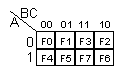
Esimerkkitaulumme kartta näyttäisi siis seuraavalta:
|
On jo huomattavasti helpompi havaita, että funktio saa arvon 1 aina, kun
muuttuja A saa arvon 1. Tämän lisäksi taulusta nähdään, että funktio saa arvon
1, kun C= 1 ja B'=1. |
Lisää Karnaugh'n kartan käyttöohjeita seuraavilla sivuilla.
Luento 4
Lisätietoja: