Sivukartta
Sanasto
Laskuharjoitukset
Funktion sieventäminen ja käsittely
Mahdollisimman kannattavan piiritoteutuksen aikaansaamiseksi pyritään sieventämään looginen funktio yksinkertaisimpaan
olemassa olevaan muotoonsa. Funktion voi sieventää joko totuustaulusta tai lausekkeesta. Lausekkeesta
sieventäminen on suoraviivaisempaa. Siihen käytetään suoraan Boolen algebraa (eli kytkentäalgebraa). Tietokone
apuvälineenä on suotavaa, mutta pienet lausekkeet voidaan hyvin sieventää käsin.
Sievennysesimerkki F = X'YX' + XZ'Y' + Z'XY:
F = X'YX' + XZ'Y' + Z'XY
F = X'YX' + XZ'Y' + Z'XY
= X'Y + XZ'Y' + Z'XY ¦ perustelu: AA=A
= X'Y + XZ'Y' + Z'XY
= X'Y + XZ'Y' + XZ'Y ¦ perustelu: AB = BA (kommutatiivisuus sääntö)
= X'Y + XZ'Y' + XZ'Y
= X'Y + XZ'(Y + Y') ¦ perustelu : AB + AC = A(B+C) (distributiivisuus sääntö)
= X'Y + XZ'(Y + Y')
= X'Y + XZ' ¦ koska A + A' = 1
Kaikki sieventäminen perustuu suoraan "Kytkentäalgebran teoreemoja"-sivulla esitettyihin sääntöihin. Alle on koottu pari vinkkiä, joita tarvitaan usein:
- sulut saa kertoa auki ja yhdistellä samoin kuin tavallisessa algebrassa
- AA = A samoin kuin AAAA = A (eli saman muuttujan monikerrat voi poistaa)
- A + A' saa aina arvon yksi (koska A + A' on aina 1 + 0 tai 0 + 1)
- AA' saa aina arvon nolla (koska AA' on aina 1*0 tai 0*1)
Konsensusteoreema
Konsensusteoreema on hyödyllinen lausekkeita yksinkertaistettaessa. Se sanoo seuraavaa:
AB + A'C + BC = AB + A'C. Eli vasemmanpuoleisen lausekkeen viimeinen termi on tarpeeton.
Tämä siksi, että termi B aiheuttaa funktion ulostuloksi ykkösen silloin kuin A on yksi. Toisaalta
termi C pakottaa funktion arvon ykköseksi silloin kun A on nolla. Tällöin nämä kaksi termiä sisältävät
tapauksen BC.
Teoreema voidaan todistaa helposti joukko-opilla. Kuten joukko-opista on jo lukiossa opittu, vastaa kahden funktion JA-operaatio kahden joukon leikkausta (eli niiden yhteistä aluetta), sekä kahden joukon TAI-operaatio vastaa kahden joukon unionia (eli niiden molempien täyttämää aluetta yhdessä)
Esimerkki selventänee asiaa:
| yhtälön vasen puoli | yhtälön oikea puoli | |||||
|---|---|---|---|---|---|---|
| joukko | kuva | joukko | kuva | |||
| lähtötilanne A, B, C | 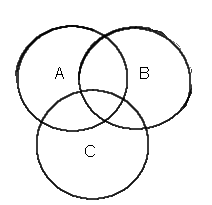 | lähtötilanne A, B, C |  | |||
| (leikkaus) AB | 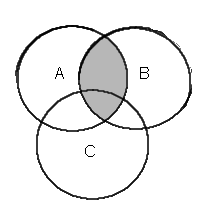 | (leikkaus) AB |  | |||
| (leikkaus) A'C | 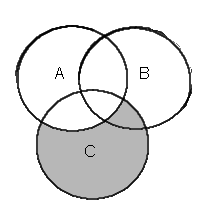 | (leikkaus) A'C |  | |||
| (leikkaus) BC | 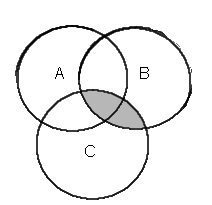 | Tämä termi (BC) jää pois turhana, sillä se vain värjää toiseen kertaan jo värjätyn alueen. | ||||
| (unioni edellisistä leikkauksista) AB+A'C+BC Huomataan, että tummennettu osa kuvassa on värjätty kaksi kertaa eli turhaan. | 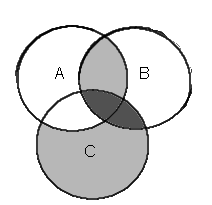 | (unioni edellisistä leikkauksista) AB+A'C | 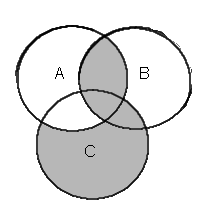 | |||
Näin ollen termin BC voi siis jättää pois, koska olemme saaneet määriteltyä saman alueen ilmankin sitä.
Lausekkeen komplementointi
Toisinaan tarvitaan jonkin kokonaisen funktion komplementtia. Tällöin käytetään De Morganin teoreemaa yleisessä
muodossa:
-komplementoidaan kaikki muuttujat ja
-vaihdetaan TAI operaatiot JA operaatioiksi ja päinvastoin.
Esimerkkinä komplementoidaan lauseke F = AB' + C(A + B').
F = AB' + C(A + B')
F' = (A' + B)(C' + A'B) - eli TAI-operaatiot ovat muuttuneet JA-operatioiksi. Lisäksi kaikki muuttujat on komplementoitu (Mikäli muuttuja on valmiiksi komplementoitu muuttuu se normaaliksi uudelleen komplementoitaessa esim. A' --(komplementointi)--> A''= A
Tämä voidaan johtaa myös peruskaavojen perusteella:
F' = (AB' + C(A + B'))'
= (AB')'(C(A + B'))' ¦ perustelu: (X+Y)' = X'Y'
= (A' + B'')(C' +(A + B')') ¦ perustelu: (XY)' = X'+Y'
= (A' + B)(C' + A'B) ¦ perustelu: X'' = X
Luento 4
Lisätietoja: