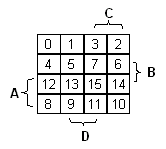
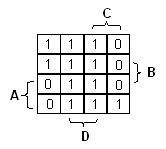
Ensimmäiseksi sijoitetaan funktion arvot Karnaugh'n karttaan. Muistin virkistämiseksi vasemalla alla esitetään mikä totuustaulun rivi tulee mihinkin ruutuun. (Sääntö: muuten vasemmalta oikealle, ylhäältä alas; paitsi kaksi oikeanpuoleista saraketta sekä kaksi alinta riviä vaihtavat keskenään.

! HUOM ! Edellä mainittu sääntö rivien sijoittamisesta ruutuihin pätee ainoastaan, mikäli muuttujat (nyt A,B,C ja D) määrittävät juuri ne alueet kuin esimerkeissä on näytetty. Toisinsanoen, mikäli menet vaihtamaan Karnaugh'n kartassa esim. B:n ja C:n alueiden paikkoja, ei edellämainittu sijoittelusääntö enää päde.)

Oikeanpuolimmaisessa kuvassa funktion arvot on sijoitettu paikoilleen.

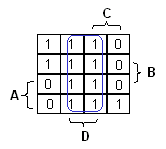
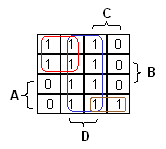
Tarkastellaan karttaa ja etsitään lauseketta funktiolle. Perussääntö on, että mitä suurempi yhtenäinen alue voidaan saavuttaa, sen parempi, sillä sitä enemmän lauseke yksinkertaistuu. Nähdään, että funktio saa arvon 1 kahdella pystyrivillä. Näillä muuttuja D saa myös arvon 1. Voidaan valita rivit suoraan, jolloin saadaan funktion ensimmäinen termi: F = D + ..

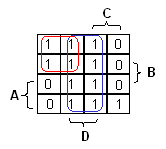
Jatketaan vaikka vasemman yläkulman ykkösillä. Kaksi ykköstä voisi valita yksinään, mutta se ei ole kannattavaa: mitä suurempi alue saadaan valittua, sitä vähemmän muuttujia tarvitaan termiin. (Mitä vähemmän muuttujia sitä yksinkertaisempi toteutus.) Toisaalta samoja ruutuja voi valita uudelleen. (Ei siis haittaa, jos funktio saa arvon yksi useammalla kuin yhdellä perusteella.) Näillä perustein voidaan ryhmitellä neljä vasemman yläreunan ruutua alueeksi ja antaa näille peruste A'C'.

Jäljelle jää enää siis yksi kiusallinen ykkösruutu oikeaan alanurkkaan. Jos tähän viitataan yksinään, vaatii se kaikkien neljän muuttujan käytön: AB'CD'. (Voi helposti todeta, että termi on juuri tuo esim. rengastamalla alueet A, B', C, D' ja katsomalla, että ruutu jäi ulkopuolelle.) Kannattaa yhdistää ruutu viereisen kanssa, jolloin saadaan kolmen muuttujan termi: AB'C.