Sivukartta
Sanasto
Laskuharjoitukset
Karnaugh'n kartan käyttö, kun halutaan POS -lauseke
(POS lauseke on siis Product Of Sums eli summien tulo.)
POS tapauksessa kannattaa muistaa, että POS lauseke perustuu maksimitermeihin.
(Niihin funktiota kuvaaviin termeihin, jotka saavat aina arvon yksi paitsi
'omalla' totuustaulun rivillään, jolloin niiden arvo on nolla. Ks. 'Kytkentäfunktion perusmuodot'-kohtaa aiemmin.) POS -lauseke
muodostetaan funktion komplementin eli nolla-alueiden avulla.
Säännöt, joiden mukaan edetään:
Aluksi toimitaan kuten SOP -tapauksessa eli
- Laaditaan totuustaulu speksien mukaan, jollei totuustaulua ole annettu jo valmiiksi.
- Piirretään totuustaulua vastaava Karnaugh’n kartta eli tarkistetaan muuttujien määrä ja tehdään sen mukaan oikean kokoinen kartta
- Siirretään totuustaulusta ykköset karttaan rivejä vastaaviin ruutuihin ja tarkastellaan kartan nollia.
- Muodostetaan vierekkäisistä nolla-alueista mahdollisimman suuria alueita, samaan tapaan kuin SOP-tapauksessa haettiin ykkösiä
- Muodostetaan lauseke kuten SOP-tapauksessakin. Huom ! Tämä muodostettu lauseke on nyt funktion komplementoitu lauseke siis F'
- Muodostetaan summatermien looginen tulo: Tämä saadaan muodostettua komplementoimalla F' De Morganin säänöillä. Tällöin saadaan POS-muotoinen lauseke
Kannattaa muistaa, että saatu esitys ei välttämättä ole yksikäsitteinen.
Esimerkkinä POS lausekkeen muodostaminen neljällä muuttujalla.
Käytetään samaa totuustaulua kuin POS -tapauksessa.
|
Muodostetaan Karnaugh'n kartta: (Tämä osuus on siis täysin sama kuin SOP toteutuksessa.)
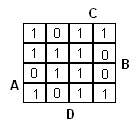
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Muodostetaan nolla-alueet ja niiden perusteella funktion lauseke (De Morganoimalla nollia ympyröimällä saatu F':n lauseke):
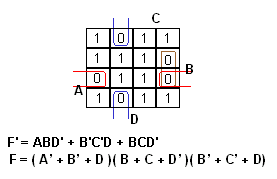
|
Luento 4
Lisätietoja: